[next] [prev] [prev-tail] [tail] [up]

5.3 Minimalflächenproblem

PIC

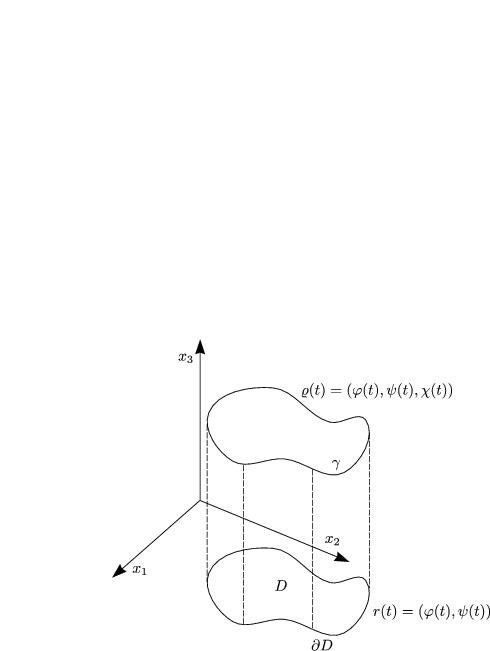
Gesucht ist eine Fläche F mit @F = g mit minimalem Flächeninhalt. Gesucht ist y = y(x1,x2) (- C1(D) mit y|@D = g, für die der Flächeninhalt minimal wird:

integral integral V~ --------- F (y) = 1 + y2x1 + y2x2 d(x1,x2) D

Überprüfe, ob F auf D [strikt] konvex ist. Ist dies der Fall, können wir die EULERsche Gleichung aufstellen.

F (y + v)- F(y)>!dF (y;v) A v (- D0(v|@D = 0)

Wir berechnen zunächst die GATEAUX-Ableitung:

integral integral dF(y;v) = [fz .v +fp .Dv] d(x1,x2) D

Unsere Funktion hängt von zwei unabhängigen Veränderlichen ab:

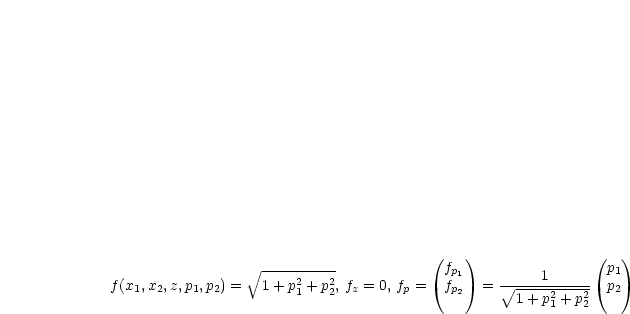
( ) ( ) V~ ---------- fp1 1 p1 f(x1,x2,z,p1,p2) = 1+ p21 + p22, fz = 0, fp = fp2 = V~ ----2---2- p2 1+ p1 + p2

integral integral yx1vx1 + yx2vx2 dF(y;v) = V~ 1-+-y2-+-y2-d(x1,x2) D x1 x2

Es muß nun gelten:

V~ --------------------- V~ ---------- y V~ x1vx1 +-yx2vx2 < 1+ (y+ v)2x + (y+ v)2x - 1 + y2x + y2x 1+ y2x1 + y2x2 1 2 1 2

Wir multiplizieren mit dem Nenner durch und formen um:

||||( 1 ) ||||||||( 1 ) |||| 2 V~ ----------- V~ --------------------- |||| yx1 |||||||| (y+ v)x1 |||| 1+yx21+yx2+yx1vx1+yx2vx2 < 1+ y2x1 + y2x2 1+ (y+ v)2x1 + (y+ v)2x2 = |||| yx2 |||||||| (y+ v)x2 |||| |||| |||||||| ||||

Auf der linken Seite steht gerade das Skalarprodukt dieser Vektoren, womit gilt:

( ) ( ) ||( )|| ||( ) || 1 1 |||| 1 |||| |||| 1 |||| yx1 . (y + v)x1 < |||| yx1 |||| |||| (y + v)x1 |||| yx2 (y + v)x2 |||| yx2 |||| |||| (y + v)x2 |||| || || || ||

Dies ist die Cauchy-Schwarzsche Ungleichung, womit die Aussage gilt. Gleichheit liegt vor, falls beide Vektoren linear abhängig, sprich Vielfache voneinander sind:

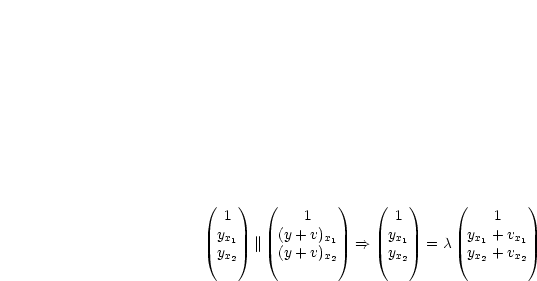
( ) ( ) ( ) ( ) 1 1 1 1 yx1 (y + v)x1 yx1 yx1 +vx1 yx2 || (y + v)x2 ==> yx2 = c yx2 +vx2

Aus der ersten Zeile folgt c = 1. Daraus wiederum ergibt sich vx1 = 0 und vx2 = 0. Damit ist v(x1,x2) = const. = D. Wegen v(x1,v2) = 0 für (x1,x2) (- @D erhalten wir v = 0. F ist damit auf D strikt konvex.

Nun ist die EULER-LAGRANGE-Gleichung zu lösen. Gesucht ist y (- D mit dF(y;v) = 0 A v (- D0. Wir setzen nun der Übersichtlichkeit halber:

U = V~ ---yx1-----, W = V~ ---yx2----- 1+ y2x1 + y2x2 1+ y2x1 + y2x2

Daraus folgt dann mit dF(y;v) = 0:

integral integral integral integral 0 = [U vx1 + W vx2] d(x1,x2) = [((Uv)x1 + (W v)x2) - Ux1v- Wx2v] d(x1,x2) = D |_ ( ) D _| ( ) integral integral Uv integral U v integral integral = |_ \~/ . W v - v(Ux1 + Wx2) _| d(x1,x2) = W v .do- v(Ux1 + Wx2) d(x1,x2) = 0 A v D @D D
(5.1)

Der erste Term verschwindet, daß v|@D = 0 ist. Damit der zweite Term gleich Null ist, muß auf D gelten:

Ux1 + Wx2 = 0

Daraus ergibt sich dann folgende partielle Differentialgleichung:

|------------------------------------------------------| |yx1x1(1+ y2x2)- 2yx1yx2yx1x2 + yx2x2(1+ y2x1) = 0, (x1,x2) (- D -------------------------------------------------------

|--------------------------------------------| -Randbedingung: y(f(t),y(t)) =-x(t)--(y|@D-=-g)|

Hierbei handelt es sich um eine nichtlineare partielle Differentialgleichung, deren Lösung sehr aufwändig ist. Das gute an der Gleichung ist jedoch, daß nur Ableitungen vorkommen, aber nicht die Funktion y selbst. Es sei nur erwähnt, daß diese Gleichung mittels der Legendre-Transformation gelöst werden kann.

[next] [prev] [prev-tail] [front] [up]