
![]() sei die Dichte, welche wir als konstant annehmen. Es ist also das Minimum der
potentiellen Energie zu finden:
sei die Dichte, welche wir als konstant annehmen. Es ist also das Minimum der
potentiellen Energie zu finden:

Die Randbedingung für dieses Problem ist, daß die Länge der Kurve konstant ist:

Betrachten wir zuerst allgemein das Funktional F, welches auf ![]() minimal werden
soll:
minimal werden
soll:

Mit folgender Nebenbedingung:
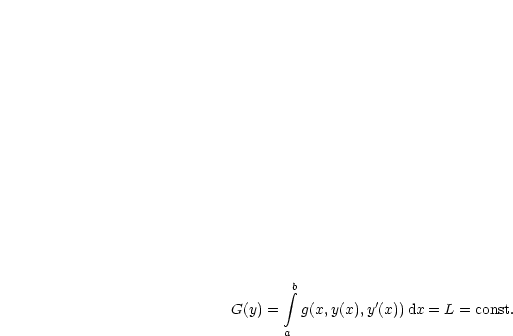
Betrachte mit ![]() = const. das Hilfsfunktional:
= const. das Hilfsfunktional:
Wiederholen wir an dieser Stelle den Satz 3:

Die Fläche sei ![]() (x,y,z) = 0. Gesucht ist die Kurve auf F. Dann sind folgende
Randbedingungen möglich:
(x,y,z) = 0. Gesucht ist die Kurve auf F. Dann sind folgende
Randbedingungen möglich:
Es sei ![]() = {y
= {y ![]() C1[0,1]|y(0) = y(1) = 0} gegeben. Auf D soll dann folgendes
Funktional minimiert werden:
C1[0,1]|y(0) = y(1) = 0} gegeben. Auf D soll dann folgendes
Funktional minimiert werden:

Das zweite Funktional, welches eine Fläche unter der Kurve darstellt, ist nun gerade unsere Nebenbedingung G(y). Dann betrachten wir:
![integral 2
F(y) = F (y)+ cG(y) = [y'(x)2 + cy(x)]dx auf D
0](ma476x.gif)
Da wir die Summe einer konvexen (z) und einer stark konvexen Funktion (p2) haben
ist f stark konvex und ![]() strikt konvex. Durch Lösung der EULERschen Gleichung
erhalten wir also eine eindeutige Lösung des Problems.
strikt konvex. Durch Lösung der EULERschen Gleichung
erhalten wir also eine eindeutige Lösung des Problems.
Daraus folgt die Differentialgleichung:
Wir suchen hier nun Lösungen auf ![]() , also mit y(0) = y(1) = 0. Durch Integration
erhalten wir zwei Integrationskonstanten, welche wir mit den Randbedingungen
bestimmen:
, also mit y(0) = y(1) = 0. Durch Integration
erhalten wir zwei Integrationskonstanten, welche wir mit den Randbedingungen
bestimmen:
Aus der Nebenbedingung kann nun ![]() bestimmt werden:
bestimmt werden:
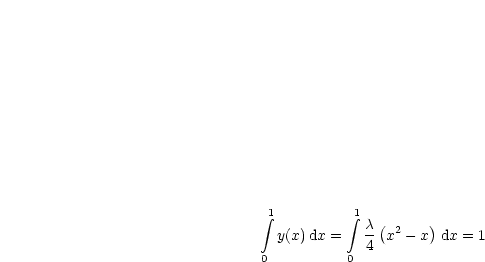
Dies ergibt dann ![]() = -24 und durch Einsetzen in obige Funktion y(x) folgt
schlußendlich:
= -24 und durch Einsetzen in obige Funktion y(x) folgt
schlußendlich:
Es ist das Minimum auf ![]() zu bestimmen von:
zu bestimmen von:
![x
integral 2[ V~ ------ V~ ------]
F (y) = rgy(x) 1+ y'2 + c 1+ y'2 dx
x1](ma485x.gif)
Dieses Funktional ist jedoch nicht konvex, womit unsere vorherigen Erkenntnisse nur bedingt anwendbar sind. Formen wir den Ausdruck deshalb so um, daß er konvex wird. Wir verändern die unabhängigen Veränderlichen.

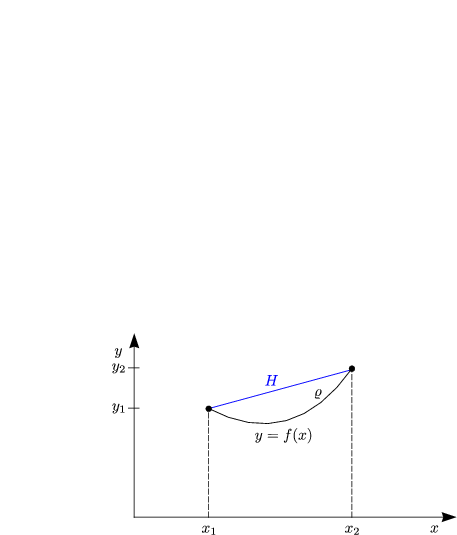
Die Länge der Kette sei L. Die unabhängigen Variablen längs der gesuchten Kurve sei
die Bogenlänge s. Gesucht sind x(s) und y(s) für 0 < s < L. Es ist also folgendes auf
![]() = {y
= {y ![]() C1[0,L]|y(0) = y(L) = 0} zu minimieren:
C1[0,L]|y(0) = y(L) = 0} zu minimieren:

Unter der Nebenbedingung:
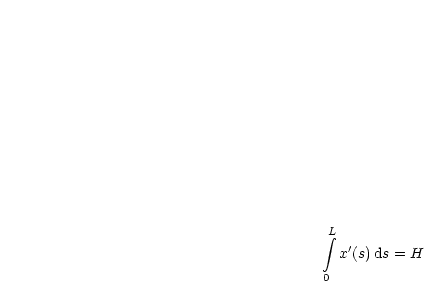
Wegen x'(s)2 + y'(s)2 = 1 (siehe Definition der Bogenlänge, HMII) ergibt sich für die Nebenbedingung:
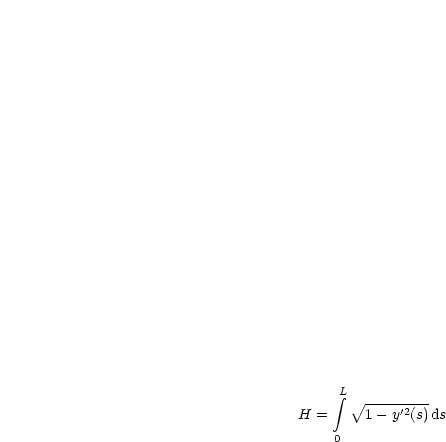
Aus x'(s)2 + y'(s)2)1 folgt, daß |y'(s) < 1 ist für 0 < ![]() < L. Aus y'(s) = 1 folgt
y'(s) = 0; die Kurve würde also senkrecht zur x-Achse stehen. Wir hätten somit eine
Spitze in der Kurve und dies ist physikalisch nicht sinnvoll. Betrachten wir
nun:
< L. Aus y'(s) = 1 folgt
y'(s) = 0; die Kurve würde also senkrecht zur x-Achse stehen. Wir hätten somit eine
Spitze in der Kurve und dies ist physikalisch nicht sinnvoll. Betrachten wir
nun:
![integral L[ V~ --------]
F(y) = y(s)+ c 1- y'2(s) ds
0](ma490x.gif)
Ist dieser Ausdruck konvex? Dazu betrachten wir:
z ist als lineare Funktion konvex und ![]()
![]() ist für
ist für ![]() < 0 stark konvex. Damit ist
die Summe aus beiden Funktionen stark konvex und F strikt konvex. Wenn
wir also jetzt die EULERsche Gleichung lösen, haben wir ein eindeutiges
Minimum.
< 0 stark konvex. Damit ist
die Summe aus beiden Funktionen stark konvex und F strikt konvex. Wenn
wir also jetzt die EULERsche Gleichung lösen, haben wir ein eindeutiges
Minimum.
y = y(s) ist symmetrisch um s = ![]() . Es gilt daher y'
. Es gilt daher y'![]() = 0. Dann bilden
wir:
= 0. Dann bilden
wir:
Die EULERsche Gleichung resultiert dann sofort:
Mit der Randbedingung y'![]() folgt die Konstante C =
folgt die Konstante C = ![]() . Wir quadrieren uns lösen
nach y'(s)2 auf:
. Wir quadrieren uns lösen
nach y'(s)2 auf:
Für y'(s) < 0 erhalten wir:

Mit y(0) = 0 ergibt sich mittels einer Integraltabelle (beispielsweise BRONSTEIN):
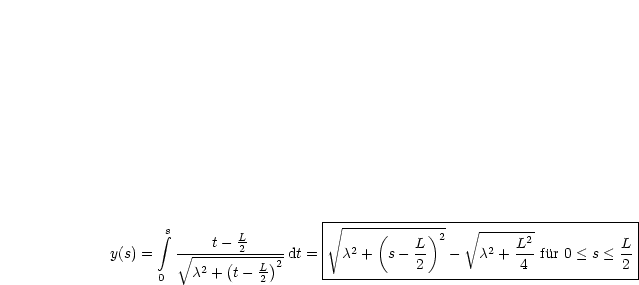
Mittels der Nebenbedingung erhalten wir für 0 < s <![]() :
:
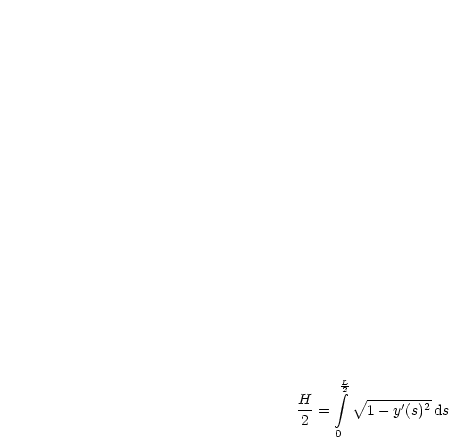
Daraus und mit y(s) ist dann ![]() < 0 zu eliminieren. Mittels der EULERschen
Differentialgleichung können wir die Wurzel eliminieren:
< 0 zu eliminieren. Mittels der EULERschen
Differentialgleichung können wir die Wurzel eliminieren:

Gibt es nun ein ![]() < 0, so daß dies gilt? Setzte nun
< 0, so daß dies gilt? Setzte nun ![]() = -
= -![]() und betrachte das
Integral g(
und betrachte das
Integral g(![]() ):
):

Mit der Regel von de l’Hospital ergibt sich nach mühsamer (!) Rechnung:
Da g stetig und mit g'(![]() ) > 0 streng monoton wachsend auf [0,
) > 0 streng monoton wachsend auf [0,![]() ] ist, wird nach
dem Zwischenwertsatz jeder Wert zwischen 0 und
] ist, wird nach
dem Zwischenwertsatz jeder Wert zwischen 0 und ![]() genau einmal angenommen.
Wegen H < L gibt es genau ein
genau einmal angenommen.
Wegen H < L gibt es genau ein ![]() 0 mit
0 mit ![]() = g(-
= g(-![]() 0). Mit diesem
0). Mit diesem ![]() 0 erhält
man:
0 erhält
man:
Mit x'(s) + y'(s)2 = 1 erhält man:
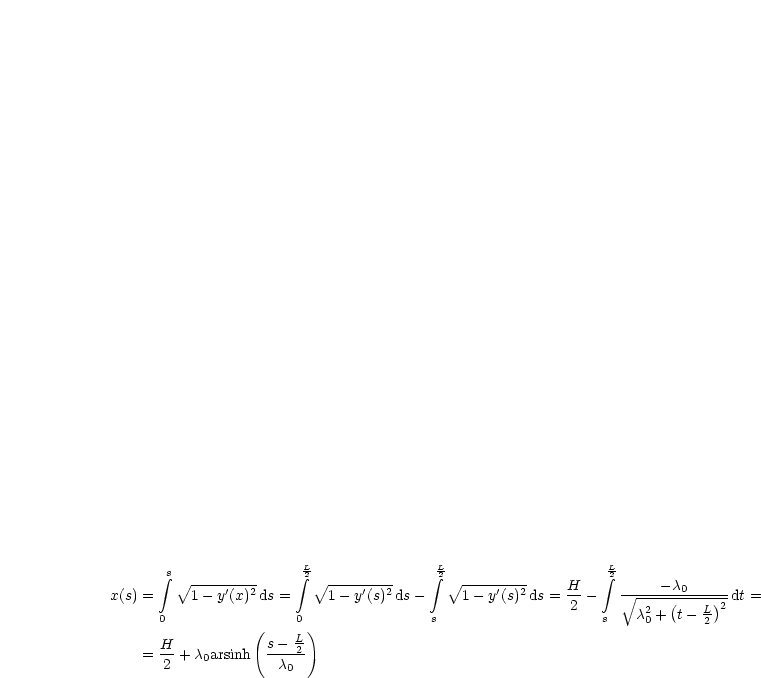 | (5.2) |
Wobei wir wissen, daß das ![]() 0 einer Gleichung genügt, welche wir lösen können. Wir
fassen zusammen:
0 einer Gleichung genügt, welche wir lösen können. Wir
fassen zusammen:

Aus der Beziehung für x erhalten wir außerdem:
Daraus erhalten wir schließlich die explizite Darstellung:
