6.8 Zum isoperimetrischen Problem

Das klassische isoperimetrische Problem ist, wie groß der maximale Flächeninhalt ist, welcher von einer Kurve gegebener Länge L berandet wird. Wir wollen an dieser Stelle jedoch nicht dieses Problem, sondern eine Variante dessen betrachten, nämlich das sogenannte Sehnen-Bogen-Problem.

Hierbei ist die Kurve der Länge 2L gesucht, welche die Punkte P₁, P₂ einer Ebene so verbindet, daß die von dieser Kurve und der Geraden P₁P₂ umschlossene Fläche maximal wird. Damit soll also folgendes Funktional auf D = {y ¹[0,2a] (Es können also Ecken auftreten.) maximal werden:

integral 2a F(y) = ydx mit y(0) = 0 und y(2a) = 0 0

Unter der Nebenbedingung konstanter Bogenlänge 2L:

2 integral p G(y) = V~ 1-+-y'2-dx = 2L mit G(x) > 0 0

Gesucht sind stationäre Funktionen des Funktionals (y) auf ¹[0,2a] mit y(0) = y(2a) = 0 und y(x) > 0:

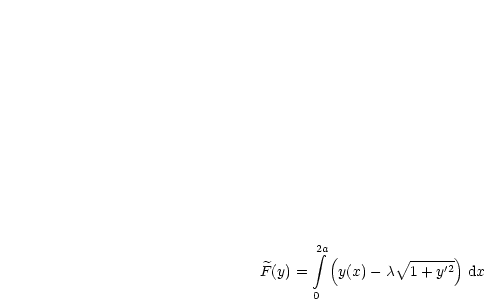
integral 2a( V~ ------) F (y) = y(x)- c 1 + y'2 dx 0

= const. ist der LAGRANGEsche Multiplikator. Gehen wir so vor wie immer:

V~ ------ f(x,z,p) = z- c 1 +p2

' fp(x,y(x),y'(x)) = -c V~ -y(x)--, fz = 1 1+ y'(x)2

EULERgleichung E1: $( ' ) -d- -c V~ -y-(x)--- = 1 dx 1 + y'(x)2$
EULERgleichung E1:
Mit U(x,z,p) = f - pf_p wollen wir außerdem E2 angeben:
$d V~ --------- y'(x) --U = 0 <==> y(x)- c 1+ y'(x)2 +y'(x)c V~ ----'--2-= C dx 1+ y (x)$
Daraus ergibt sich durch Zusammenfassen:
$y(x)- c V~ ---1-----= const. 1+ y'(x)2$

Setzen wir nun y' = tan(), womit gilt:

[ ] V~ ---1-----= cosy f¨ur y (- 0, p 1+ tan2y 2

Damit können wir E2 folgendermaßen umschreiben:

y(x)- C = ccosy

dx = cot(y) dy = cot(y)(- c)sin(y)dy = - cos(y) dy

Damit erhalten wir x und y in Abhängigkeit von :

y(y)- C1 = ccos(y)

x(y)- C2 = - csin(y)

|----------------------| (x - C2)2 + (y - C1)2 + c2 ------------------------

Es liegt damit ein Kreis mit Radius || vor. Durch Auswerten der Randbedingungen y(0) = y(2a) = 0 resultiert nun:

C22 + C21 = c2

(2a - C2)2 + C21 = c2

4a2- 4aC2 = 0 ==> C2 = a ==> c2 = C2 + a2 1

Außerdem gilt ja die Nebenbedingung, nämlich daß die Länge der Kurve konstant sein muß:

2 integral p V~ --------- 1+ y'(x)2 dx = 2L 0

y'(x)2 = --(x--a)2--- c2- (x- a)2

Durch Einsetzen in die Nebenbedingung und anschließendes Integrieren ergibt sich:

|------------(--)| |2L = 2c arcsin a- | --------------c---

Es stellt sich außerdem die Frage, ob es Funktionen mit Ecken gibt. Dazu untersuchen wir die Eckenbedingungen:

--p----- --p+---- -c V~ ----2-= -c V~ ----2- 1+ p- 1+ p+

1 1 1 1 y(c)- c V~ ----2-= y(c)- c V~ -----2 ==> V~ ----2-= V~ ----2-= a 1+ p- 1 + p+ 1+ p+ 1- p-

Damit folgt aus der ersten Gleichung -p_- = -p₊ und damit p_- = p₊; es treten folglich keinerlei Ecken auf. Fassen wir unsere Ergebnisse nochmal zusammen:

(x- a)2 + (y- C1)2 = c2, c2 = C21 + a2

(a ) a L = c arcsin c- = ca, sina = c-

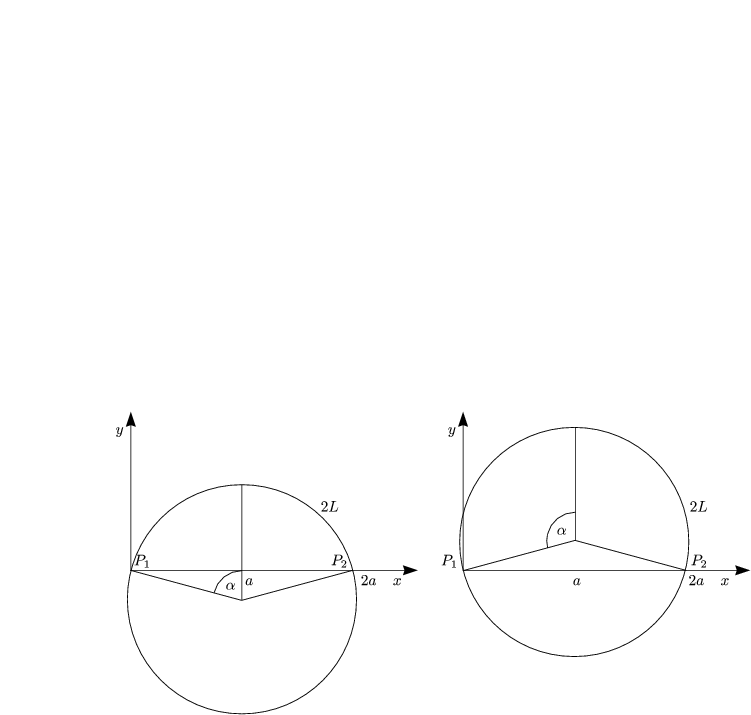
Der zweite Fall wird bei dieser Untersuchung nicht erfaßt, daß es sich sonst um keine Kurve der Form y = (x) handelt. Mit solchen Fällen, werden wir uns im nächsten Kapitel näher beschäftigen.

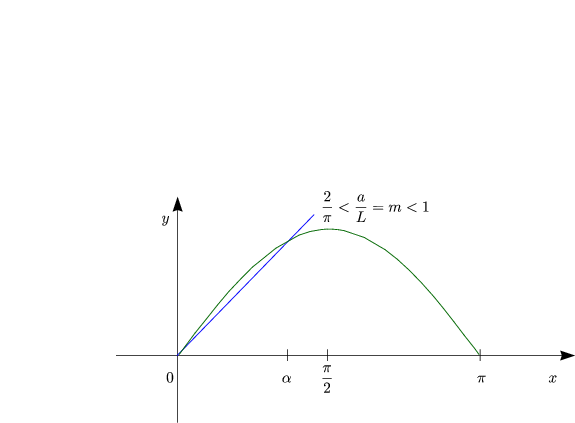
Es gilt nun L = . Aus = und sin = ergibt sich dann = . Die Behauptung ist nun, das diese Gleichung für ein erfüllt wird. Hierbei handelt es sich um eine transzendente Gleichung, welche wir dazu geometrisch untersuchen wollen:

y = mx = ax L

y = sin(x)

2-< a-< 1 und L 2-< a < L p L p

|---------p--| |aa = L < 2a | -------------

Für = erhalten wir gerade einen Halbkreis. Dies ist der letzte mögliche Fall der Form y = (x). Man kann nun außerdem diese extremale Fläche A in Abhängigkeit von (wie vorher bestimmt) angeben, was hier jedoch nicht hergeleitet werden soll:

|------------------------| | ( a ) | |Amax = a2 sin2a-- cota | -------------------------

[prev] [prev-tail] [front] [up]