6.7 Minimaloberflche eines Rotationskrpers

6.7 Minimaloberfläche eines Rotationskörpers

Es liege folgendes Funktional vor:

integral b F (y) = f(x,y(x),y'(x))dx a

Hier gilt ¹, also N = 1, y ², also n = 2 und schließlich y'(x) = ² mit nN = 2.

( ) ( ) y1(x) y'1(x) y(x) = y2(x) , y'(x) = y'2(x)

Es liegt also f = f(x,z,p) = f(x,z₁,z₂,p₁,p₂) vor. Damit können wir die erste EULERsche Gleichung (E1) aufschreiben:

|-------------------------------------| | integral x | fp(x,y(x),y'(x)) = fz(t,y(t),y'(t)) dt+ C | | a | ---------------------------------------

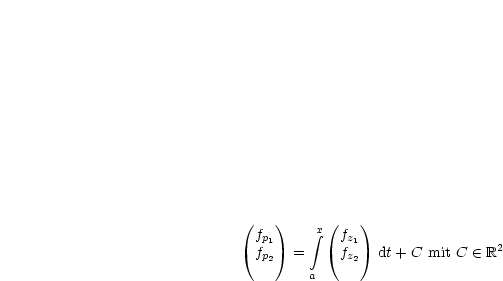
( ) ( ) fp1 integral x fz1 fp2 = fz2 dt+ C mit C (- R2 a

Durch Differentiation folgt:

d-- ' ' dxfp(x,y(x),y(x)) = fz(x,y(x),y (x))

Außerdem schreiben wir die zweite EULERsche Gleichung (E2) auf. Dazu benötigen wir die Funktion U(x,y(x),y'(x)):

U (x,y(x),y'(x)) = f(x,y(x),y'(x))- y'(x).fp(x,y(x),y'(x))

Der zweite Term auf der rechten Seite beschreibt ein Skalarprodukt. Für dieses U gilt dann:

---------------------------------- |d | |dxU (x,y(x),y'(x)) = fx(x,y(x),y'(x)) ----------------------------------

Darüber hinaus brauchen wir die Eckenbedingungen (Stetigkeit von f_p und von U) an.

Ohne Beschränkung der Allgemeinheit nehmen wir außerdem b₁ > 1 an, was ja auch durch Drehung des Rotationskörpers erreicht werden kann. die gesuchte Kurve wird in Parameterform dargestellt:

x = x1(t), y = x2(t) mit 0 < t < 1

( ) ( ) ( ) x1(t) 0 b r(t) = x2(t) mit r(0) = 1 , r(1) = b1

Allgemein gilt für die Fläche eines Rotationskörpers:

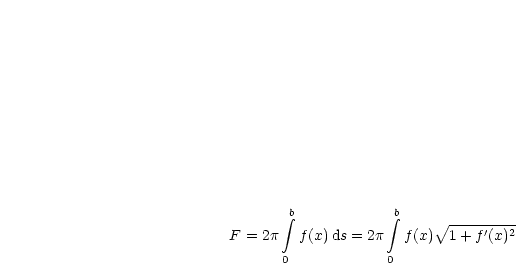
integral b integral b V~ --------- F = 2p f (x)ds = 2p f(x) 1 +f '(x)2 0 0

Durch Umrechnung von der expliziten Darstellung in die Parameterdarstellung erhalten wir:

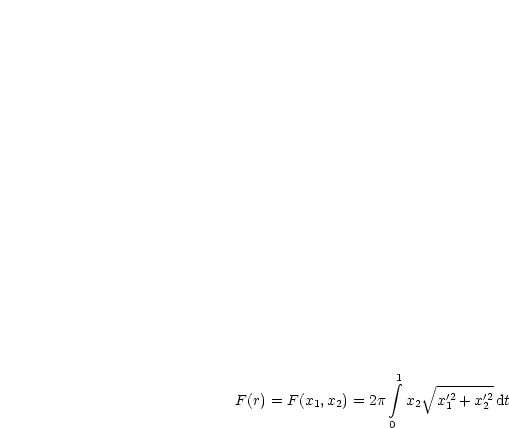
integral 1 V~ -------- F (r) = F(x1,x2) = 2p x2 x'21 + x'22dt 0

Dieses Funktional ist also auf D = $( ) ( ) { ( )2 0 b } r (- C^1[0,1] | r(0) = 1 ,r(1) = b1$ zu minimieren. Damit können wir jetzt die EULERschen Gleichungen für dieses Problem formulieren. Es gilt:

V~ ----- f = f(t,z1,z2,p1,p2) = z2 p21 + p22

Erste EULERsche Gleichung: $( ) ( ) fp1 z2 p1 ' ' ' x2 ' fp = fp2 = V~ p2-+-p2 p2 , fp(t,x1(t),x2(t),x1(t),x2(t)) = fp(t,r(t),r(t)) = ||r'(t)||r(t) 1 2$

$( ) ( ) ( ) fz1 V~ --0--- 0 fz = fz2 = p21 + p22 , fz(t,r(t),r'(t)) = ||r'(t)||$
Damit lautet E1:
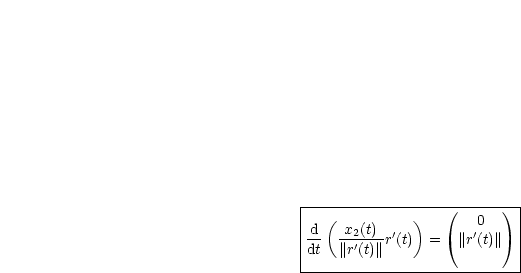
$|--------------------------| | ( ) ( 0 ) | -d -x2(t)-r'(t) = ||r'(t)|| | dt ||r'(t)|| | ----------------------------$
Zweite EULERsche Gleichung: $( ) ( ) V~ -2---2 p1 ---z2--- p1 U(t,z,p) = z2 p1 + p2- p2 . V~ p2-+-p2 p2 = 0 1 2$
Damit ist die zweite EULERsche Gleichung immer erfüllt; es gilt nämlich die wahre Aussage 0=0.

Beschäftigen wir uns also ausschließlich mit E1, wobei wir diese komponentenweise aufschreiben wollen:

[ ' ] [ ' ] -d x2(t)'x1(t)- = 0,-d x2(t)'x2(t)- = ||r'(t)|| dt --||r (t)||-- dt --||r(t)||-- fp1 fp2

Notieren für uns die Eckenbedingungen. Liegt bei t_c eine Ecke, so sind (t) und (t) bei t_c stetig.

' ' q(t) = x2(t)x1(t), j(t) = x2(t)x2(t) ||r'(t)|| ||r'(t)||

Auf glatten Stücken einer Extremalen gilt:

x2(t)x'(t) -||r'(t1)||---= C0 = const.mit 0 < t < 1

1.Fall: x₂ oder x₁' sind Null für ein t [0,1].
Daraus ergibt sich dann C₀ = 0 und damit verschwinden x₂ oder x₁' auf glatten Stücken von Extremalen.
Wir haben also folgende Kurven, welche man auch als Goldschmidt-Kurven bezeichnet:
2.Fall: C₀0
Für alle t [0,1] sind x₂(t)0 und x₁'(t)0. (t) und (t) sind stetig. Damit ist stetig auf [0,1]. Die gesuchte Kurve hat keine Ecken. Infolgedessen gehen wir aus von r = r(t) ². Es gilt für C₀0:
$[ ] x2(t)2x'1(t)2 2 d- x2(t)x'2(t) ' ||r'(t)|| 2 = C0 und dt ||r'(t)|| = ||r (t)||$
Wir multiplizieren die zweite Gleichung mit und wir erhalten:
$1d (x2 (t)x'2(t)) 1 d 2dt -2||r'(t2)||2- = 2dtx22(t)$
Somit kann die Zeitableitung weggelassen werden:
$2 '2 x2x-2 (t)-= x22(t)+ C1 ||r'(t)||2$
Durch Addition der ersten ursprünglichen Gleichung mit dieser ergibt sich schließlich:
$x22(t) = x22(t) +C20 + C1$
Es muß damit C₀² = -C₁ gelten. Wir können diese Gleichungen außerdem durcheinander dividieren:
$x'22- x22- C1- x'21 = C20 - 1, da - 1 = C20$
Mit y = (x) und x₂(t) = (x₁(t)) erhalten wir ' = . x₁' ist stetig und 0. Weiterhin gilt:
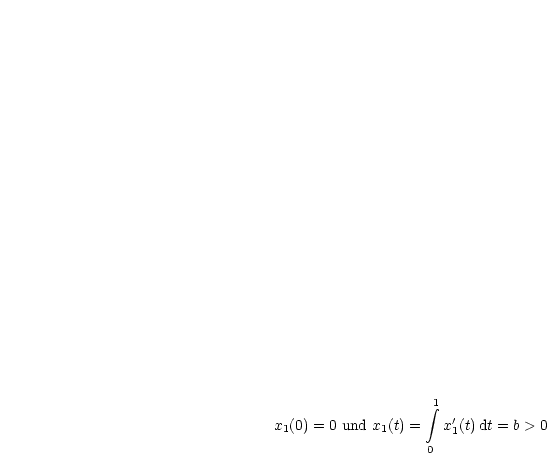
$integral 1 ' x1(0) = 0 und x1(t) = x 1(t)dt = b > 0 0$
Um von (0,0) nach (b,b₁) zu gelangen, muß die Steigung auf jeden Fall positiv sein, wenn wir keinen Vorzeichenwechsel haben; es gilt also x₁'(t) > 0 für t [0,1]. x = x₁(t) besitzt damit eine C¹-Inverse t = x₁^-1(x).
$y = x2(t) = x2(x-11(x)) =: f(x) (- C1[a,b]$
Es resultiert also, daß die Lösungskurve in expliziter Form der Klasse C¹[a,b] mit (0) = 1, (b) = b₁ gesucht werden kann. Die Differentialgleichung ² = - 1 wird zu '(x)² = ²(x) - 1 (mit ²(x) > C₀² und (x) > 0). Setze (x) = C₀ cosh(v(x)).
$v'2C2 sinh2(v(x)) = cosh2(v(x))- 1 = sinh2(v(x)) 0$

$1 1 v'(x)2 = -2-==> v(x) = --x + m C0 C0$
Daraus folgt schlußendlich:
$|----------------(-------)-| | x-- | |y = f(x) = C0cosh C0 + m | ---------------------------$
Es muß nun (0) = 1 und (b) = b₁ gelten. Damit erhalten wir:
$1 1 = f(0) = C0cosh(m), C0 = cosh(m)$

$y = f(x) = cosh(xcosh(m)-+-m) cosh m$

$cosh(bcosh(m)+ m) y(b) = b1 =----cosh(m)---- (*)$
Gesucht ist also bei gegebenem b und b₁(> 1). Es sei (*) erfüllt. Es gilt cosh(t) > |t| t. Dies kann man folgendermaßen zeigen:
$cosh(t) = 1 (exp(t)+ exp(- t)) 2$

$t3 t5- 1 sinh(t) = t+ 3! + 5! + ...= 2 (exp(t) -exp(- t)) > t f¨ur t > 0$
Daraus ergibt sich cosh(t) > sinh(t) > t für t > 0 und somit cosh(t) > t für t > 0. Es sei nun t < 0: Dann gilt cosh(-t) > -t. Da cosh(t) eine gerade Funktion ist, gilt außerdem cosh(-t) = cosh(t) und wir erhalten damit durch Zusammenfassen der beiden Ungleichungen für t > 0 und t < 0, daß cosh(t) > |t| ist. Mit (*) und der eben gezeigten Ungleichung gilt:
$|bcosh(m)+ m| |b cosh(m)|- |m| |m| b1 > ---cosh(m)--- > ---cosh(m)--- = b- cosh(m)-> b- 1$
Notwendig für die Erfüllung von Gleichung (*) ist also die Bedingung b₁ > b - 1. Gilt jedoch b₁ < b - 1, so gibt es keine stetig differenzierbaren Lösungen (Goldschmidt-Kurven).
Genauere Diskussionen dieses Problems findet man in [1], [4] und [11].

[next] [prev] [prev-tail] [front] [up]