7.1 EULERgleichungen bei Problemen in Parameterdarstellung

Eine Eigenschaft der EULERgleichungen

Für N = 2 gilt:

Die Voraussetzung ist, daß y C² sein muß. Die Homogenitätsrelation war

Wir gehen aus von einer Lösung y = y(t) C² von (E). Aus Gleichung (H) ergibt sich:

Führen wir die Differentiation aus:

(7.2)

Schreiben wir dies komponentenweise auf:

Da (t)0 ist, gilt entweder ₁(t)0 oder ₂(t)0, woraus folgt:

Wenn man eine der beiden EULERschen Gleichungen gelöst hat, so bringt die zweite EULERsche Gleichung keine zusätzlichen Informationen; die beiden EULERschen Gleichungen sind voneinander abhängig. Man sucht sich infolgedessen zur Lösung immer die einfachere Gleichung!

Beispiel:

• F(y) = _a^by²(x)y'²(x)dx

  Wir wollen dieses in ein Problem in Parameterdarstellung umformen:

  
  

  Dann gilt für die EULERsche Gleichung:

  
  

  Wir zuvor schon erwähnt, reicht es nun, eine der beiden Gleichungen zu lösen. Zur Übung wollen wir aber beide lösen:

  • Erste Gleichung:
    

    Durch Integration erhalten wir:

    

    Mit y = y₂(t) und x = y₁(t) ergibt sich y²(x) = 2C₁x + C₂. Hierbei handelt es sich um eine Parabelschar.

  • Zweite Gleichung:
    
    

    Mit y₂0 ergibt sich:

    

    Hieraus folgt y₂(t)₂(t) = C₁₁(t) und damit dasselbe wir vorher.

Beispiel:

Wir betrachten das Funktional:

Hiermit können geodätische Linien in der Ebene berechnet werden. Es gilt f(z,p) = ||p||. Dann gilt die EULERsche Gleichung:

Es folgt hiermit durch Integration:

Wir erhalten durch Division der beiden Gleichungen:

Mit = C₃ erhalten wir (t) = C₃(t) + C₅ (x = C₃y + C₅), also eine Gerade.

Beispiel:

Es soll folgendes Funktional minimiert werden:

Wir betrachten alle Kurven in der Ebene durch die Punkte A und B mit der Länge 2L, welche den maximalen Flächeninhalt einschließen.

Es handelt sich um eine Variante des isoperimetrischen Problems.

Um die EULERsche Gleichung aufstellen zu können, benötigen wir:

f_p2 und f_z2 folgt analog. Damit gilt für die erste EULERsche Gleichung:

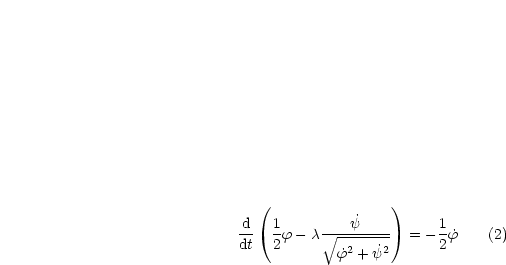
Gleichung (1) ist äquivalent zu:

Gleichung (2) sieht analog aus:

Der Betrag dieser Größe ist die sogenannte Krümmung der Kurve. Die Krümmung ist also konstant, was nur für einen Kreis mit Radius || der Fall ist.

• Fall || > |AB|:

  

  Man erhält zwei Kreise.

• Fall || = |AB|:

  

  Man erhält einen Halbkreis.

• Fall || < |AB|

  Es gibt keine Lösung.

Man kann auch so vorgehen: Aus Gleichung (1) ergibt sich unter anderem:

Und aus Gleichung (2):

Man kann die erste Gleichung mit und die zweite mit multiplizieren und dann beide Gleichungen addieren. Dann fällt der Term mit der Wurzel heraus und die entstandene Gleichung ist einfach zu lösen. Eine andere Möglichkeit ist folgende:

Durch Quadrieren und Addieren erhält man nun sofort die Kreisgleichung:

Hieraus ergibt sich C₁ = 0, also a² + C₂² = ².

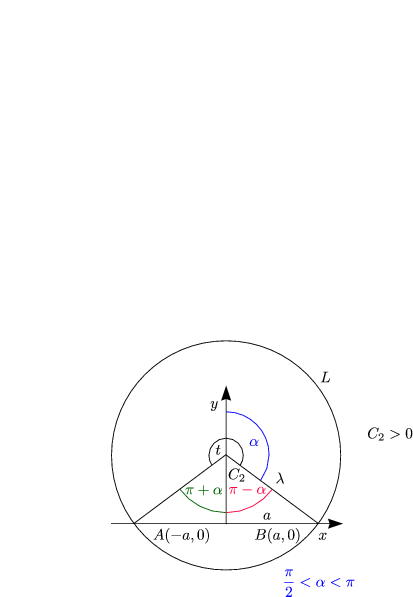
Mit L = und a = sin ergibt sich:

Im Falle C₂ < 0 erhalten wir:

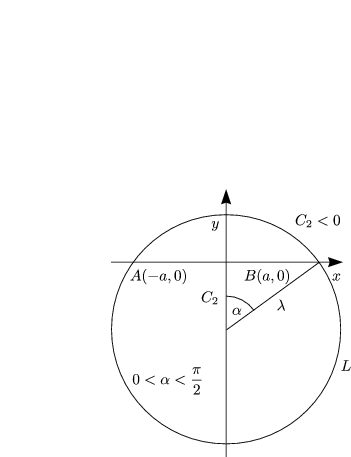
Es gilt C₂ = -cos. Dann folgt:

Dann läßt sich auch der maximale Flächeninhalt bestimmen:

• a = : Halbkreis mit Radius a
• a = : Vollkreis mit Radius a