

auf einer geeigneten Menge D minimiert. Wir betrachten folgendes Funktional, welches minimal werden soll:

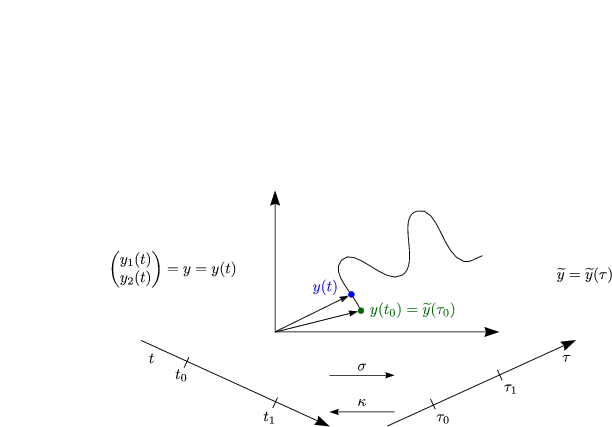
Sei y(t) = ![]() , t0 < t < t1 eine Lösung. y(t) beschreibt eine Kurve K. Es sei
, t0 < t < t1 eine Lösung. y(t) beschreibt eine Kurve K. Es sei
![]() (
(![]() ) =
) =  ,
, ![]() 0 <
0 < ![]() <
< ![]() 1 auch eine Darstellung der Kurve K. Das Problem
oben ist nur sinnvoll gestellt, falls der obige Integralausdruck unabhängig von der
speziellen Parameterdarstellung ist, das heißt falls gilt:
1 auch eine Darstellung der Kurve K. Das Problem
oben ist nur sinnvoll gestellt, falls der obige Integralausdruck unabhängig von der
speziellen Parameterdarstellung ist, das heißt falls gilt:

Betrachten wir folgende Parametertransformation:

Wir haben damit folgende zulässige Parametertransformation:

Es gelte (I).
![integral s integral r
f(t,y(t), ˙y(t))dt = f(t,y(t),y'(t))dt ( A s (- [t0,t1])
t0 t0](ma885x.gif)
Wir führen die Substitution t = ![]() (
(![]() ) durch:
) durch:
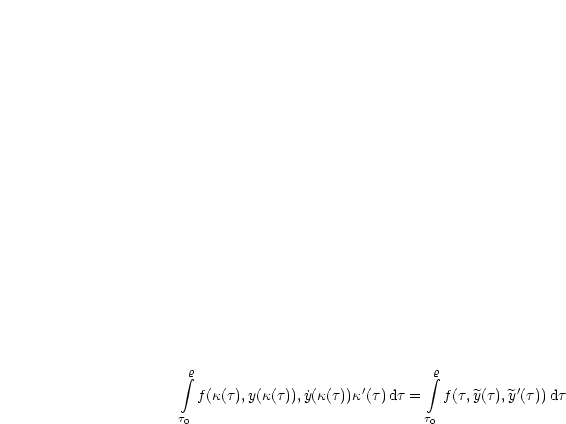

Dies gilt für jedes zulässige ![]() und jedes
und jedes ![]()
![]() [
[![]() 0,
0,![]() 1]:
1]:
Wähle nun x(![]() ) =
) = ![]() (
(![]() + c) (mit
+ c) (mit ![]() > 0 beliebig und c
> 0 beliebig und c ![]()
![]() beliebig):
beliebig):
Wir setzen ![]() = 1 und differenzieren nach c:
= 1 und differenzieren nach c:
Mit c = 0 erhalten wir:
Wir haben Aussage 1.) bewiesen.
![integral s integral r
f(t,y(t), ˙y(t))dt = f(t,y(t),y'(t))dt ( A s (- [t0,t1])
t0 t0](ma893x.gif)
Ab jetzt sei f = f(z1,z2,p1,p2). Dann ergibt sich:
Es gilt also auch 2.). i
Zu zeigen ist dann (I):

Aus 1.) ergibt sich dann:

Ab jetzt lautet das Variationsintegral

f genüge der Homogenitätsbedingung 2.). Dann ist das Problem, ein Minimum von F(y) zu finden, unabhängig von speziellen Parameterdarstellungen (geometrische Variationsprobleme).

Es gilt hier nun f(z,p) = ||p|| und f(z,![]() p) =
p) = ![]() ||p|| für
||p|| für ![]() > 0.
> 0.
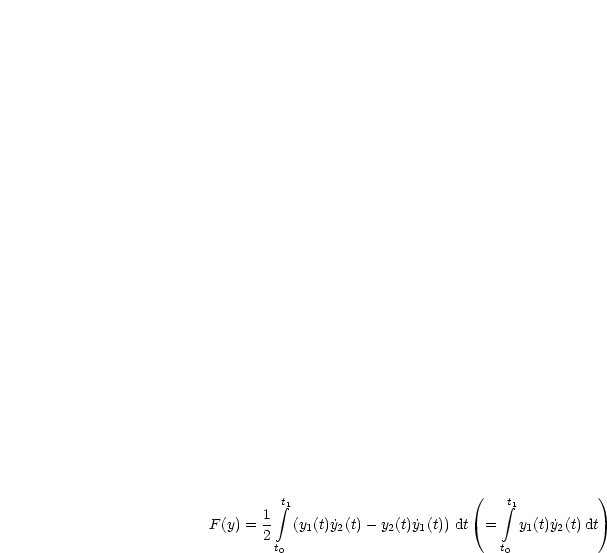
f(z1,z2,p1,p2) = ![]() (z1p2 - z2p1) hat die Eigenschaft 2.).
(z1p2 - z2p1) hat die Eigenschaft 2.).


Dieses soll auf D = {y ![]()
![]() 1[0,1],y(0) = y(1) = 0} minimiert werden.
Aus
1[0,1],y(0) = y(1) = 0} minimiert werden.
Aus ![]() (y) > 0 ergibt sich, daß y(x) = 0
(y) > 0 ergibt sich, daß y(x) = 0 ![]() D das Minimum liefert. Das
zugeordnete parametrische Problem ist:
D das Minimum liefert. Das
zugeordnete parametrische Problem ist:

Ohne Beschränkung der Allgemeinheit setzen wir t1 = 1 und t0 = 0:


Als Übung kann man für 0 < h < 1 zeigen:
Die einfachsten Parameterdarstellungen dieser Geraden sind:
Das nichtparametrische Problem sei:
![integral 1
F (y) = y'2(x)dx, D = {y (- C^1[0,1],y(0) = 0,y(1) = 1}
0](ma914x.gif)
Mit f(x,z,p) = p2 folgt aus fpp = 2 > 0 Konvexität. Damit ist die Lösung der EULERgleichung das Minimum.

Die Lösung ist y(x) =. Daraus folgt ![]() (y(x) = x) = 1. Schauen wir uns außerdem das
parametrische Problem an:
(y(x) = x) = 1. Schauen wir uns außerdem das
parametrische Problem an:

Dieses kann beliebig negativ gemacht werden durch Verbindungskurven von (0,0) und (1,0).
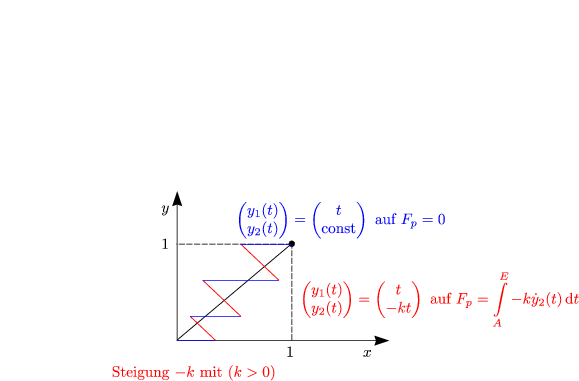
Für ein diagonales Stück gilt:
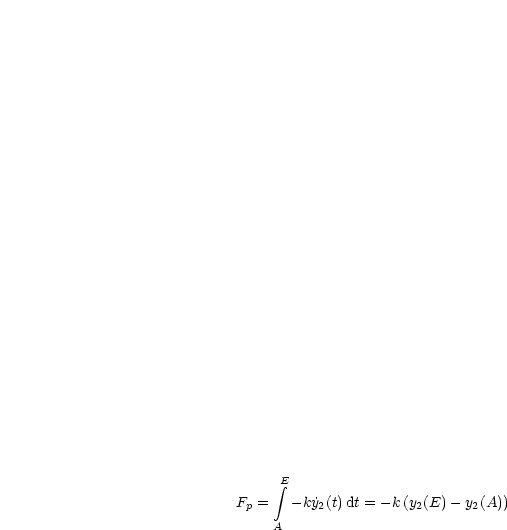
Insgesamt ergibt sich dann durch Addition aller solcher Teilstücke:

Für g(x) = x.y gilt g(![]() x) = (
x) = (![]() x) .y =
x) .y = ![]() (x.y) =
(x.y) = ![]() g(x). Damit gilt k = 1.
g(x). Damit gilt k = 1.
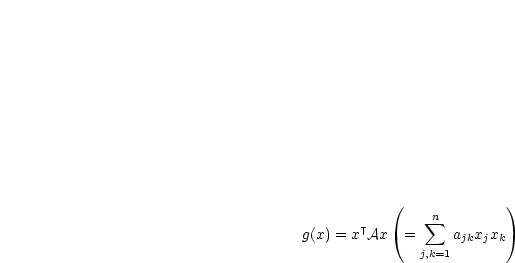
Damit gilt für eine quadratische Form k = 2.
|
| (7.1) |
A kann als symmetrische Matrix angenommen werden.
Der letzte Schritt folgt aus x![]() (A-A
(A-A![]() )x
)x![]() 0.
0.

Es sei x ![]()
![]() N fest. Betrachte für
N fest. Betrachte für ![]() > 0 die Funktion h(
> 0 die Funktion h(![]() ) = g(
) = g(![]() x) für
x) für ![]() > 0. Wir
gehen von einer positiv homogenen Funktion aus: g(
> 0. Wir
gehen von einer positiv homogenen Funktion aus: g(![]() x) =
x) = ![]() kg(x). Durch
Differentiation erhalten wir h'(
kg(x). Durch
Differentiation erhalten wir h'(![]() ) =
) = ![]() .
.![]() g(
g(![]() x) = k
x) = k![]() k-1g(x). Für
k-1g(x). Für ![]() = 1 folgt dann die
Behauptung.
= 1 folgt dann die
Behauptung.
Gegeben ist x .![]() g(x) = kg(x) für x
g(x) = kg(x) für x ![]()
![]() N. Wir schreiben die Voraussetzung für
N. Wir schreiben die Voraussetzung für ![]() x
hin:
x
hin:
Wir betrachten ![]() (
(![]() ) = g(
) = g(![]() x) -
x) -![]() kg(x). Wir leiten eine Differentialgleichung her, von
der wir wissen, daß sie nur die triviale Lösung hat:
kg(x). Wir leiten eine Differentialgleichung her, von
der wir wissen, daß sie nur die triviale Lösung hat:
![]() genügt also der Differentialgleichung
genügt also der Differentialgleichung ![]() '(
'(![]() ) =
) = ![]()
![]() (
(![]() ). Deren Lösung ist
). Deren Lösung ist
![]() (
(![]() ) =
) = ![]() k
k![]() (1) = 0. Aus
(1) = 0. Aus ![]() (1) = 0 ergibt sich
(1) = 0 ergibt sich ![]() (
(![]() ) = 0
) = 0 ![]()
![]() .
.
Wir betrachten F(y) = ![]() t0t1
f(y(t),
t0t1
f(y(t),![]() (t))dt mit f(z,p), wobei f(z,
(t))dt mit f(z,p), wobei f(z,![]() p) =
p) = ![]() f(z,p)
gilt, f(z,p) also positiv homogen vom Grad 1 ist. Aus Satz 2 folgt dann:
f(z,p)
gilt, f(z,p) also positiv homogen vom Grad 1 ist. Aus Satz 2 folgt dann:
Wir wiederholen an dieser Stelle einige Begriffe:
Hier gilt, wobei z ![]()
![]() N, p
N, p ![]()
![]() N und q
N und q ![]()
![]() N ist:
N ist:
Differenzieren wir dies nach p:
Wir können ![]() > 0 herauskürzen, woraus sich fp(z,
> 0 herauskürzen, woraus sich fp(z,![]() p) = fp(z,p)
ergibt oder auch fp(z,
p) = fp(z,p)
ergibt oder auch fp(z,![]() p) =
p) = ![]() 0fp(z,p). fp ist bezüglich der p-Variablen
homogen vom Grade 0. Durch Anwenden von Satz 2 ergibt sich 0 =
p . fpjp(z,p) für j = 1, 2, ..., N.
0fp(z,p). fp ist bezüglich der p-Variablen
homogen vom Grade 0. Durch Anwenden von Satz 2 ergibt sich 0 =
p . fpjp(z,p) für j = 1, 2, ..., N.

fpp ist die HESSEmatrix bezüglich der p-Variablen.
![|----------------------------------------------------------------------------------------|
| |
|Es sei y = y(t) eine schwache ^C1-Extremale von F mit ||y(t)|| = 1 f¨ur t0 < t < t1. Des weiteren sei
|E(y(t), ˙y(t),q) > 0 f¨ur alle t (- [t0,t1] und alle q /= c˙y(t) (c > 0). Dann gilt y (- (C1[t0,t1])N. |
-----------------------------------------------------------------------------------------](ma949x.gif)
Wir betrachten:
Wähle ![]()
![]() (t0,t1) beliebig. In diesem Punkte berechnen wir p :=
(t0,t1) beliebig. In diesem Punkte berechnen wir p := ![]() (
(![]() - 0)
und q :=
- 0)
und q := ![]() (
(![]() + 0). (Das Ziel ist, zu zeigen, daß p = q gilt.) Bekannt ist
fp(y(
+ 0). (Das Ziel ist, zu zeigen, daß p = q gilt.) Bekannt ist
fp(y(![]() ),p) = fp(y(
),p) = fp(y(![]() ),q). Damit gilt:
),q). Damit gilt:
Hieraus ergibt sich p = ![]() q mit
q mit ![]() > 0 und außerdem ||p|| =
> 0 und außerdem ||p|| = ![]() ||q||. Mit ||p|| = ||q|| = 1
ergibt sich
||q||. Mit ||p|| = ||q|| = 1
ergibt sich ![]() = 1 und p = q, was zu zeigen war.
= 1 und p = q, was zu zeigen war.
Betrachten wir f(z,p) = ![]() (z)||p|| mit
(z)||p|| mit ![]() (z) > 0 und
(z) > 0 und ![]()
![]() C1. Für
C1. Für ![]() (z) = 1 liegt das
Bogenlängenfunktional vor:
(z) = 1 liegt das
Bogenlängenfunktional vor:

Für y ![]()
![]() 2 ergibt sich ein Funktional, welches wir früher schon bei der Behandlung
von Rotationsflächen besprochen haben:
2 ergibt sich ein Funktional, welches wir früher schon bei der Behandlung
von Rotationsflächen besprochen haben:
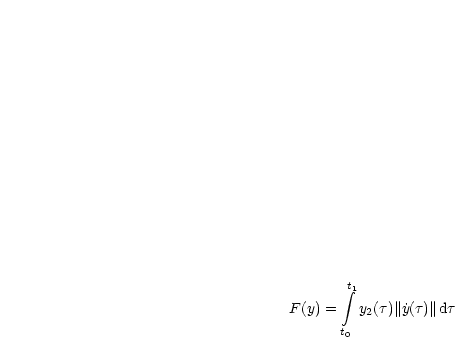
Allgemein ergibt sich für f(z,p) = ![]() (z)||p||, daß
(z)||p||, daß ![]() = p (mit ||p|| = 1)
ist.
= p (mit ||p|| = 1)
ist.
Gleichheit gilt nur für q = ![]() p mit
p mit ![]() > 0 (gleichgerichtet!). Aus q
> 0 (gleichgerichtet!). Aus q![]()
![]() p mit
p mit ![]() > 0 folgt
E(y(t),p,q) > 0. Aus Satz 4 folgt dann, daß y
> 0 folgt
E(y(t),p,q) > 0. Aus Satz 4 folgt dann, daß y ![]() C1 ist. Dann erhalten wir (Satz 3)
mit ||
C1 ist. Dann erhalten wir (Satz 3)
mit ||![]() (t)|| = 1:
(t)|| = 1:

Sowohl das Integral als auch ![]() (y(t)) sind
(y(t)) sind ![]() C1. Damit ist
C1. Damit ist ![]() (t)
(t) ![]() C1 und
y
C1 und
y ![]() C2.
C2.