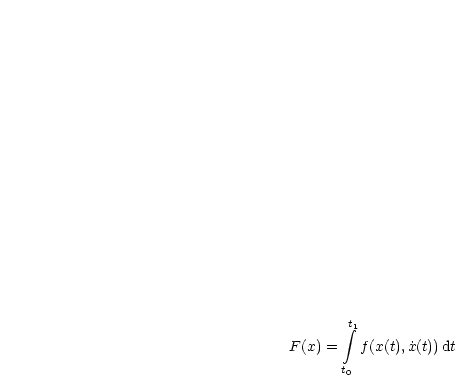
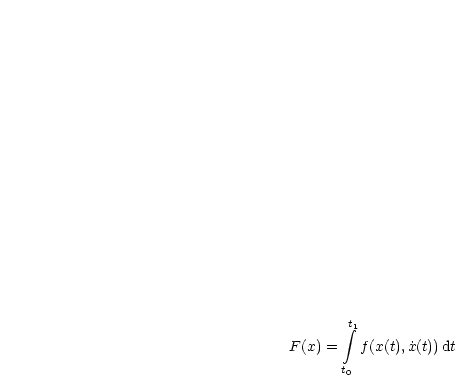
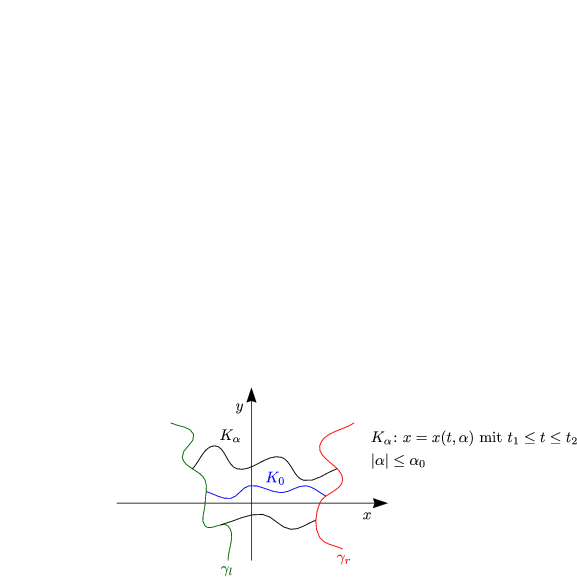
l und r seien ebene Kurven. Außerdem sei f = f(z,p) = f(z1,z2,p1,p2) 
C1
genüge der Homogenitätsbedingung. K0: x = x0(t) sei die minimierende Kurve des
Problems:
![integral t1
F(x) = f(x(t), ˙x(t))dt auf D = {x (- C1[t1,t2]| ˙x(t) /= 0 und x(t1) = gl, x(t2) = gr}
t0](ma1027x.gif)
Es sei x C1![([t1,t2]× [-a0,a0])](ma1028x.gif){kind=small}
und außerdem gelte 
(t,
) = xt(t,), 
(t,)
0 
, t (t1,t2). K0: x(t,0) = x0(t). Des weiteren sei x(t1,) l und x(t2,) r.
Die Parameterdarstellung für l sei xl() := x(t1,) und für r sei diese
xr() := x(t2,).
![|----------------------------------------------------------------------------------------|
| t2 |
| integral 2 |
|fp((x0(t), ˙x0(t)) = c + fz(x0(t), ˙x0(t))dt mit t (- [t1,t2] und c (- R = const. |
| t1 |
| |
|Es sei fp(x0(t), ˙x0(t)) =: s(t) und damit gilts˙(t) = fz(x0(t), ˙x0(t)). |
-----------------------------------------------------------------------------------------](ma1032x.gif)
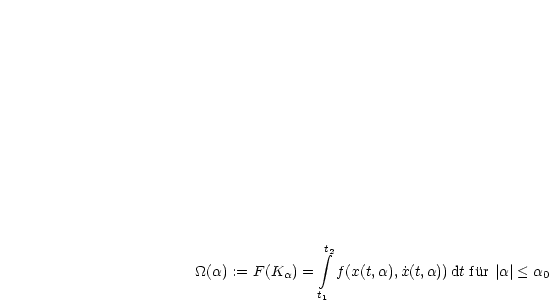
Wir berechnen 
'(0) = 0.
![t
' integral 2
_O_ (a) = [fz(x(t,a), ˙x(t,a))xa(t,a) + fp(x(t,a),x˙(t,a)).˙xa(t,a)] dt
t1](ma1034x.gif)
![integral t2
0 = _O_'(0) = [fz(x0(t),x˙0(t)).xa(t,0)+ fp(x0(t),x ˙0(t)).˙xa(t,0)] dt =
t t1
integral 2 d
= dt [s(t).xa(t)] dt = s(t2)xa(t2,0)- s(t1)xa(t1,0)
t1](ma1035x.gif) | (8.1) |
Wählen wir speziell {K
, ||< 0} mit x(t1,) = x0(t1). Hieraus folgt x(t1,0) = 0.
Damit erhalten wir die Bedingung ||
(t2) . x(t2,0)|| = 0. Wählen wir andernfalls
speziell {K, ||< 0} mit x(t2,) = x0(t2), womit x(t2,0) = 0 folgt und damit
||(t1) . x(t1,0)|| = 0. haue!
l möge die Parameterdarstellung x = xl(
) mit J haben und r die Darstellung
x = xr(
) mit I. K0: x = x0(t) mit t1 < t < t2 sei Lösungskurve des Problems. Es
sei x0(t1) = xl(
) und x0(t2) = xr(
). x = x0(t) muß die folgenden Bedingungen
erfüllen:
fp(x0(t),
0(t)) = fz(x0(t),
0(t)) für t1 < t < t2
0(t1)) . xl'(
) = 0
0(t2) . xr'(
) = 0
(y) soll nun minimal werden auf D = {y C1[a,b]|. Es gibt Zahlen l, r mit
a < l < r < b und (l,y(l)) l und (r,y(r)) r}.
Die Lösung sei K0: y = y0(x) für l < x < r. Deren Parameterdarstellung
sei:
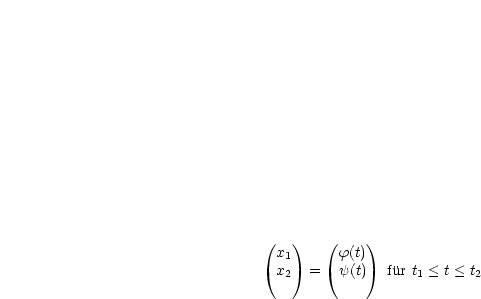
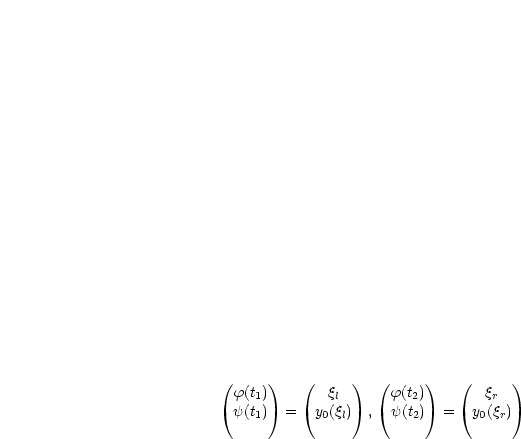
Außerdem benötigen wir:
Wir erhalten damit die Bedingung T':
Außerdem verwenden wir die üblichen Abkürzungen:
Wir können nun die Transversalitätsbedingungen für das Problem
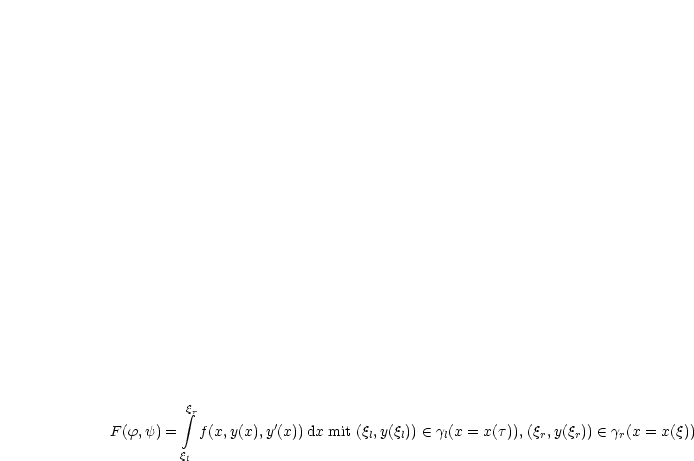
Wie sehen diese Formeln aus, falls l, r in impliziter Form gegeben sind? Es sei l:
Tl(x,y) = 0 und r: Tr(x,y) = 0.
Aus Tl(
(),
() = 0 erhalten wir durch Differentiation nach :
Hieraus ergibt sich '() = 
D2Tl und '() = -D1Tl. Hieraus folgt
T'':
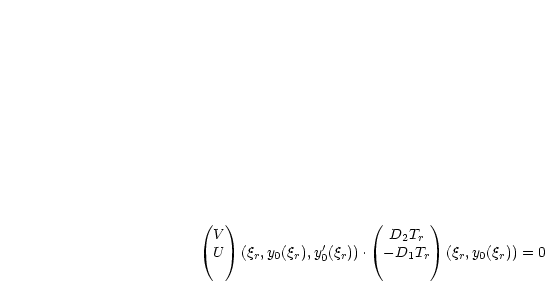
Wie sehen diese Formeln aus, falls l, r in expliziter Form gegeben sind? Es sei also
l: y = yl(x) und r: y = yr(x).
Mit D2Tl = 1 und D1Tl = -yl'(x) erhalten wir T''':
Umschreiben von T''' ergibt:
Gegeben sei L und gesucht ist die ebene Kurve durch (0,0) der Länge L, die zusammen die der x-Achse eine maximale Fläche einschließt.
Es ist l: (0,0) und gr ist die x-Achse. Rechnet man dies nach, so erhält man wie
früher den Halbkreis als Lösung.
Gesucht ist die kürzeste Verbindung von (0,0) zur Geraden y = -x + 2.
Es sei yl: (0,0) und r: (,- + 2) und damit ist das Funktional F(y) zu
minimieren:
Man kann das Problem auch in Parameterdarstellung betrachten:
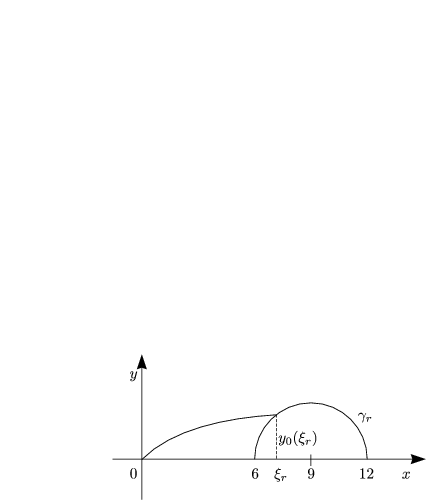
Es sei folgendes Funktional gegeben:
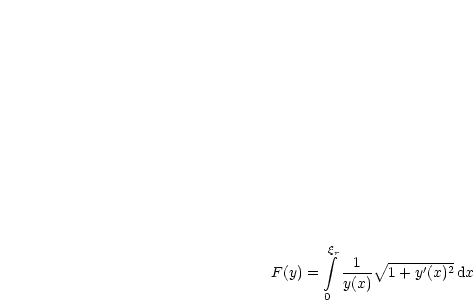
Dieses soll minimal werden mit y(0) = 0, also l: (0,0) und (r,y(r)) r:
(x - 9)2 + y2 = 9 für y > 0.
Die EULERgleichung erhält man aus:
Die Gleichung yy'' + y'2 + 1 = 0 = f(y,y',y'') löst man mit der Substitution y' = p(y) oder mit folgenden Trick: Man kann die Differentialgleichung umschreiben:
Hieraus erhält man (y2)'' = -2 und (y2)' = -2x + C1. Schließlich folgt:
Aus y(0) = 0 erhält man C2 = 0 und hieraus resultiert y2(x) = -x2 + C1x.
Mit y2 + (x - C1)2 = C22 folgt aus y(0) = 0 C12 = C22.
Wir wenden nun die Transversalitätsbedingungen (T'') auf r an:
Wir berechnen also:
 | (8.2) |
Damit erhalten wir:
Da (r,y(r)) r sein muß, gilt außerdem:
Dieses Gleichungssystem können wir lösen und erhalten C1 = 4, r = 
, y(r) = 
.
Das Ergebnis ist dann:
