3.4 Mathematischer Einschub: Komplexe Zahlen

[prev] [prev-tail] [tail] [up]

3.4 Mathematischer Einschub: Komplexe Zahlen

Reelle Zahlen:

Addition: a + b = c
Die Addition ist kommutativ.
Multiplikation: a ^. b = c
Auch die Multiplikation ist kommutativ.

Die Lösung zur Gleichung x² = 2, nämlich x = ist eine irrational Zahl. , e sind hingegen transzendent (durch Grenzwerte). Wie lautet jedoch die Lösung der Gleichung x² = -1? Die Gleichung besitzt im Reellen keine Lösung, deshalb erweitert man den Zahlenbereich und führt komplexe Zahlen ein:

2 z = x + iy, wobei x,y (- R und i = - 1

z1 .z2 = (x1 + iy1).(x2 + iy2) = (x1 .x2- y1 .y2)+ i(y1x2 +y2x1)

--1-- = ----x--iy---- = -x2--iy2- x + iy (x+ iy)(x - iy) x + y

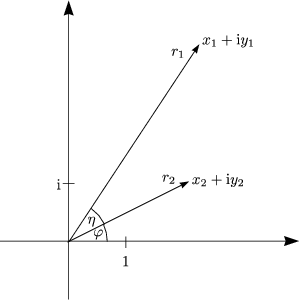
x - iy ist die konjugiert Komplexe von z. Die physikalische Lösung ist x(t) = Re(x^C(t)), also der Realteil. Der Imaginärteil i(x + y) besitzt in der Physik keine Bedeutung. Re(x^C(t)) ist auch Lösung, da die Differentialgleichung linear ist.

3.4.1 Eigenschaften von imaginären Zahlen

Betrag von z:

V~ ------- |z|= r = x2 + y2

Winkel (Argument) :

y tanf = x-

x = r cosf,y = rsinf

Eulersche Formel:

z = r(cosf+ isin-f) E(f),|E| =1

Sonstige Rechenregeln:

z1 .z2 = r1E(f1) .r2E(f2) = r1r2 (cos(f1 + f2)+ isin(f1 + f2))

|z1 .z2|= |z1|.|z2|

||z || |z | ||-1||= -1- z2 |z2|

Das heißt: E(f ).E(f ) = E(f + f ) 1 2 1 2

Die Moivresche Formel zur Berechnung von Wurzeln lautet:

zn = rn(cos(nf)+ isin(nf))

-d-E(f) = iE(f) df

Vermutung:

|---------| |E(f) = eif -----------

z z z2 zn Taylor- Reihe: e = 1+ 1! +-2! + ...+ n!-

Die Reihe konvergiert ABSOLUT:

2 1+ |z|+ |z| + ... 1! 2!

[prev] [prev-tail] [front] [up]