3.3 Oszillator mit Dämpfung (aber f(t) = 0)

[next] [prev] [prev-tail] [tail] [up]

3.3 Oszillator mit Dämpfung (aber f(t) = 0)

|-----------------------| |¨x(t)+ 2g˙x(t)+ w20x(t) = 0| ------------------------

Wir verwenden zur Lösung den Ansatz:

x(t) = A .e-ct .sin(_O_t - P)

, sind Konstanten des Ansatzes, wobei ₀ und der Dämpfungsfaktor analog für freien Fall ist.

A und sind freie Konstanten, die nicht durch die Differentialgleichung selbst festgelegt sind, sondern durch Anfangsbedingungen.

dx(t), aber nicht g(t) ==> Homogenit¨at der Zeit dt

sin_O_t(w2 - 2g2 + (-c)2)e- ct + cos_O_t(2_O_(c - g))e-ct = 0 0

F¨ur alle t : c = g,c2 = w20- g2

Schwingfall: ₀ > , = $- gt x(t) = e (C .sin_O_t + D .cos_O_t)$

$(V ~ -------) x(0) = 0,x˙(0) = v0, x(t) = V~ -v0-e-gt.sin w20- g2t lim sinx = 1 w20- g2 t'-->0 x$
Kriechfall: ₀ < $x(t) = e-ct$

$2 2 (- c) + 2g(- c)+ w0 = 0$

$V~ ------- c = g ± g2 - w2 --- --0 G$

$==> x(t) = e-gt(C .eGt + De -Gt)$

$-gt Oder: e (A.sinhGt+ B coshGt)$
Die Hyperbolikusfunktionen sind folgendermaßen definiert:
$1 (+x -x) sinhx = 2 e - e$

$1 (+x -x) coshx = 2 e + e$
Aperiodischer Grenzfall: ₀ =
Der Ansatz x = e^-t liefert nur eine Lösung = . ( - )² = 0 besitzt aber eine Doppelnullstelle. Infolgedessen ist mit e^-t auch t ^. e^-t eine Lösung.
$x(t) = (A + Bt)e-gt$

$Speziell: x(0) = 0, ˙x(0) = v0,x(t) = v0te- gt$

Periodische Funktion: f(t) = f (t+ T ),T = Periode

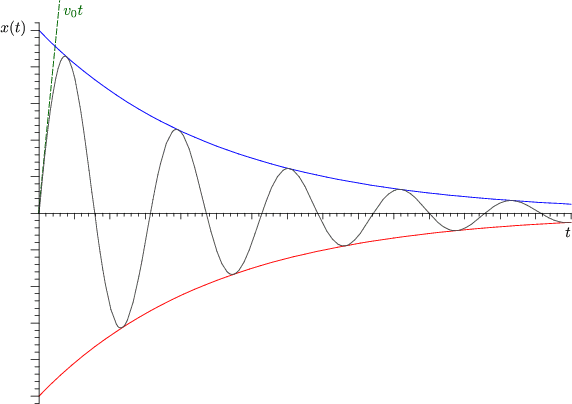
Speziell gilt:

p- f(t) = sinwt,w = T

f(t) = sin wt+ sin wt,T = 2.3 .2p 2 3 w

- f (t) = sint+ sin V~ 2t

Der allgemeine komplexe Lösungsansatz lautet:

x(t) = ect

In die Differentialgleichung eingesetzt, erhält man:

c2 + 2gc+ w20 = 0

Die Lösung dieser quadratischen Gleichung lautet:

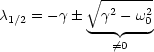
V~ ------- c1/2 = -g ± g2 - w20 --- --- /=0

Somit ergibt sich als allgmeine Lösung:

x(t) = A .ec1t + B .ec2t

Aber was ist, wenn ₁, ₂ komplex sind, also ² - ₀² < 0? Man kommt somit auf den Schwingfall:

x(t) = e-gt{A .ei_O_t + Be -i_O_t}

c1/2 = - g± i_O_,i2 = -1,i = V~ -1

[next] [prev] [prev-tail] [front] [up]