7.1 Bewegungsgleichungen

[next] [tail] [up]

7.1 Bewegungsgleichungen

x₁, x₂ sind die Auslenkungen aus der Ruhelage.

mx¨1 = -Dx1 + C(x2 - x1)

mx¨2 = -Dx2 + C(x1 - x2)

Weitere Beispiele:

Zweiatomiges Molekül:

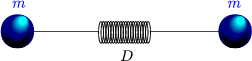
Die Feder symbolisiert die chemische Bindung.

Nachrichtentechnik, Bandfilter:

7.1.1 Mathematischer Einschub: Lineare Differentialgleichungssysteme

Wir betrachten ein lineares System von 2 gekoppelten Differentialgleichungen zweiter Ordnung mit konstanten Koeffizienten. Zur Lösung verwenden wir den Ansatz:

ct } x1(t) = a1ect c = - iw x2(t) = a2e

Beide Teilchen schwingen mit derselben Frequenz.
a₁,a₂ Amplituden noch nicht festgelegt

(-iw)2ma1 = -Da1 + C(a1 - a2)

(-iw)2ma2 = -Da2 + C(a1 - a2)

Das Gleichungssystem besteht aus 2 Gleichungen, ist linear und homogen.

(D + C -mw2)a - Ca = 0 1 2

( 2) - Ca1 + D + C - mw a2 = 0

( 2) 2 ==> D + C - mw a2- C a2 = 0 durch Einsetzen!

(( 2) 2) a2 D + C- mw - C = 0 ==> a2 = 0 triviale L¨osung

Die nichttriviale Lösung erfordert, daß

[ 2]2 2 D + C - mw - C = 0

Wir schreiben das Gleichungssystem in Matrixform:

(D + C - mw2 -C ) (a ) - C D + C- mw2 a1 = 0Determinatenmatrix = 0 -------------------------- 2 Matrix des Gleichungssystems

Wir erhalten somit die Lösung der Gleichungen für (Eigenwertgleichungen):

==> mw2 - (D + C) = ±C

V~ --- D - Zeichen: w1 = ± m-

V~ ------- +Zeichen: w = ± D--+2C- 2 m

Schwingungstyp 1:

a1 = a2

( ) ( ) a1 =~ 1 a2 1

Schwingungstyp 2:

a1 = -a2

( ) ( ) a1 =~ 1 a2 - 1

[next] [front] [up]