[prev] [prev-tail] [tail] [up]

7.4 Mathematischer Einschub: Matrix-Bezeichnung

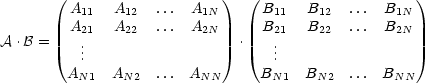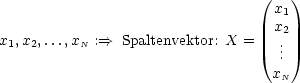
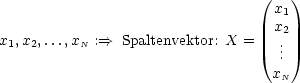
(x1 ) x2 x1,x2,...,xN :==> Spaltenvektor: X = . .. xN

7.4.1 Differentialgleichungssystem

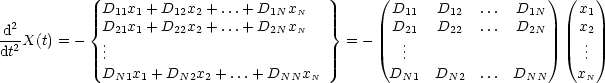
D x + D x + ...+ D x ( D D ... D ) ( x ) 2 {D 11x 1+ D12x2+ ...+ D1Nx N } D11 D 12 ... D 1N x1 -d2X(t) = - . 21 1 22 2 2N N = - 2.1 22 2N 2. dt .. .. .. DN1x1 + DN2x2 + ...+ DNN xN DN1 DN2 ... DNN xN

d2- m dt2X(t) = - DX (gleiche Massen)

Wir rechnen mit dem Ansatz X(t) = a . e-iwt wobei a ein zeitunabhängiger Vektor ist. D sei die Federkonstantenmatrix.

( ) m1 0 ... 0 M = 0 m2 ... 0 ... ... ... ... 0 0 ... mN

Mit gleichen Massen folgt:

(- iw)2a = --1Da m

( 2 ) D - w mI a = 0

7.4.2 Einheitsmatrix

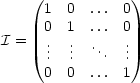
Die Einheitmatrix I sieht folgendermaßen aus:

(1 0 ... 0) 0 1 ... 0 I = .. .. .. .. . . . . 0 0 ... 1

7.4.3 Eigenwertproblem

Zu obiger Aufgabe kann folgendes Eigenwertproblem formuliert werden:
Da = ca

det(D- cI) = 0 führt auf ein Polynom N-ten Grades. In unserem Falle erhalten wir c = mw2. Zu jedem der N Eigenwerte gibt es Eigenvektoren a(j) mit j = 1, 2, ..., N.

7.4.4 Multiplikation von 2 Matrizen

( A A ... A ) ( B B ... B ) A11 A12 ... A 1N B 11 B12 ... B 1N A .B = 2.1 22 2N . .21 22 2N .. .. AN1 AN2 ... ANN BN1 BN2 ... BNN

sum N A .B = AilBlk l=1

[prev] [prev-tail] [front] [up]