Wir eliminieren die Massen:
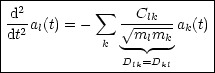
l = 1, 2, ..., f: Es handelt sich um f gekoppelte lineare Differentialgleichungen 2. Ordnung mit konstanten Koeffizienten.
Damit wäre im allgemeinen Dlk![]() Dkl und D wäre damit leider nicht
mehr symmetrisch.
Dkl und D wäre damit leider nicht
mehr symmetrisch.
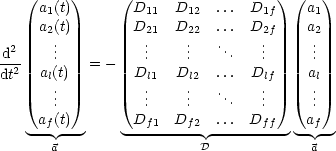
Wir bezeichnen wir ![]() Vektoren.
Vektoren.
Eigentlich gelte ak(t) = Re![]() . Dann ergibt sich durch Einsetzen und
anschließende Division durch e-i
. Dann ergibt sich durch Einsetzen und
anschließende Division durch e-i![]() t
t![]() 0:
0:
Es handelt sich um ein Eigenwertproblem mit ![]() als Eigenwert und
als Eigenwert und ![]() als zugehörigen
Eigenvektor
__________. Im allgemeinen ist D
als zugehörigen
Eigenvektor
__________. Im allgemeinen ist D![]() =
= ![]() bis auf Faktor
bis auf Faktor ![]() „Fixpunkt“.
„Fixpunkt“.
Es sind genau f Gleichungen für f Unbekannte a1, ..., af. Nichttriviale Lösungen
ergeben sich nur für spezielle ![]() . Die Bedingungen für die Bestimmung der Eigenwerte
lautet:
. Die Bedingungen für die Bestimmung der Eigenwerte
lautet:

Man bringt das Gleichungssystem auf Dreiecksform durch Addition, Multiplikation von Zeilen mit einem Skalar oder durch Vertauschen derselbigen.
Woher „weiß“ die Mathematik, daß die ![]() reell und sogar größer als 0 sind?
reell und sogar größer als 0 sind?

Die Eigenvektoren zu verschiedenen ![]() ’s sind orthogonal.
’s sind orthogonal.


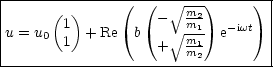
b ist eine komplexe Größe; diese enthält 2 reelle Größen. Das u0 ist reell. Dies sind nur drei Konstanten, man benötigt aber bei diesem Problem vier. Deshalb führt man die lineare Funktion u0 + v0t ein:
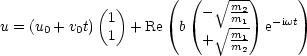
Es stellt sich hier die Frage, warum wir C = ![]() haben und nicht
C* =
haben und nicht
C* = ![]() .
.
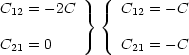
Dies ist beides richtig, aber C* ist nicht symmetrisch. Mit C* würde zwar nach wir
vor V = ![]()
![]() k,lCkl * ukul gelten, aber die Bewegungsgleichung (vergleiche Seite 42),
würde lauten:
k,lCkl * ukul gelten, aber die Bewegungsgleichung (vergleiche Seite 42),
würde lauten:
Wir spalten nun die ![]() ab:
ab:

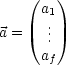
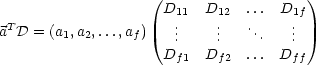
| Eigenwerte symmetrischer reeller Matrizen sind reell. |
Wir verwenden:

Der letzte Ausdruck ist somit reell!
Wir vertauschen k und l. Dann folgt mit Dkl = Dlk und anschließender Subtraktion:
Daraus resultiert nun ![]() =
= ![]() * (reell). Alternativ kann man dies auch folgendermaßen
zeigen, wobei nun * „komplex konjugiert und transponiert“ bedeutet:
* (reell). Alternativ kann man dies auch folgendermaßen
zeigen, wobei nun * „komplex konjugiert und transponiert“ bedeutet:
Mit D = D* erhalten wir dann:
Damit ist gezeigt, daß ![]() =
= ![]() * ist. Darüber hinaus gilt:
* ist. Darüber hinaus gilt:
Den nötigen Beweis hierzu gibt es auf dem nächsten Übungsblatt.
Deshalb folgt:
| Die Eigenvektoren zu verschiedenen Eigenwerten |
Transponiere Gleichung (1):
Subtrahiere Gleichungen (1) und (3) voneinander:
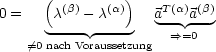
Das charakteristische Polynom hat r-fache Wurzel. Das heißt:
Es existieren r linear unabhängige Eigenvektoren, die man nach Schmidt-Verfahren orthogonalisieren kann. In unserem Fall müssen die Eigenwerte > 0 sein, das heißt, V (u1,...,uf) hat Minimum.
| In welchen gewählten Koordinaten (Normalkoordinaten) ist L eine Summe von ungekoppelten harmonischen Oszillatoren? |
Wir notieren uns dies in Komponenten:
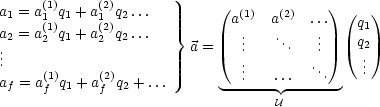
U ist die Matrix gebildet aus den Spalteneigenvektoren (normierte Eigenvektoren). Dies folgt aus der Festlegung
und außerdem aus UT = U-1.
|
|
|
|
Weiterhin gilt:
![]() hat Diagonalform.
hat Diagonalform.

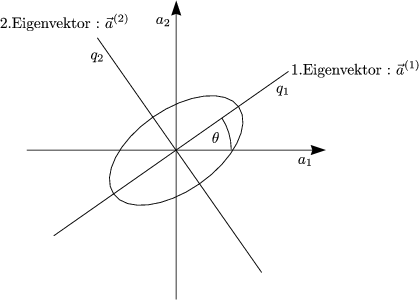
Es handelt sich somit um f ungekoppelte Oszillatoren. Die qk’s nennt man Normalkoordinaten („Modes“).
Für eine (2,2)-Matrix gilt:
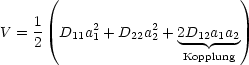
Dies ist eine sogenannte quadratische Form.