[next] [prev] [prev-tail] [tail] [up]

Kapitel 4
Gekoppelte Oszillatoren

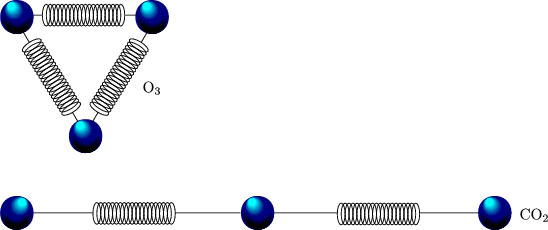
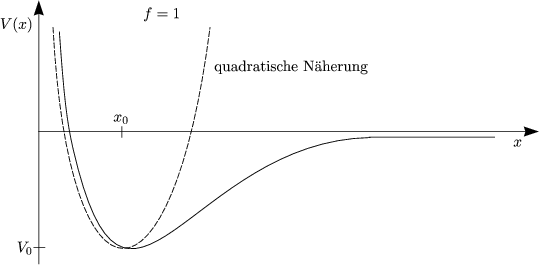
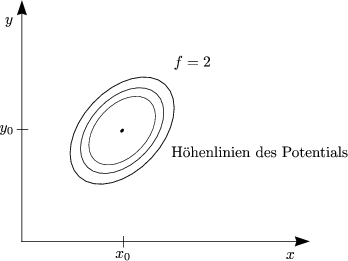
Unser Ziel ist es, Systeme mit mehreren Freiheitsgraden (d.h. N-Teilchen-Systeme) zu beschreiben. Die Bewegungen um die Gleichgewichtslagen werden als klein angenommen (kleine Amplituden). Wir werden uns zuerst den gekoppelten Oszillatoren widmen.

PIC

PIC

PIC

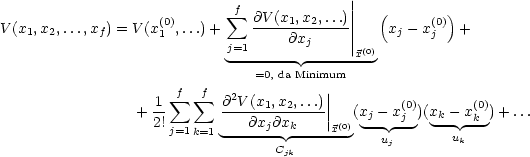f || ( ) V(x1,x2,...,xf) = V (x(0),...)+ sum @V-(x1,x2,...)|| xj -x(0) + 1 j=1 @xj || j -------- ------x(0) =0, da Minimum 1 sum f sum f @2V (x1,x2,...)|| (0) (0) + -- -------------|| (xj - xj )(xk-- xk-)+ ... 2!j=1k=1 ---@xj@xk----x(0) --uj-- uk Cjk
(4.1)
1 sum V (x1,x2,...) = V0 + 2 Cjkujuk j,k

uj = xj -xj(0) beschreiben die Auslenkungen aus den Ruhelagen. Diese sind damit generalisierte Koordinaten.

@2V (x1,x2,...)|| Cjk = ---@x-@x-----|| = Ckj Symmetrie j k x(0)

Es gilt für die Lagrange-Funktion:

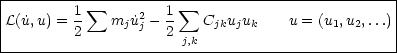
|-------------------------------------------------| | 1 sum 2 1 sum | |L(˙u,u) = 2 mj ˙uj- 2 Cjkujuk u = (u1,u2,...)| -----------------------j,k-------------------------


 4.1 Feder-Modell
  4.1.1 Matrix-Bezeichnung
  4.1.2 Charakteristisches Polynom
  4.1.3 Mathematische Eigenschaften des Eigenwertproblems
Bewegungsgleichungen für ul:
f f d- 1 sum 1 sum dt (ml˙ul) = - 2 Clkuk- 2 Cjluj k=1 j=1

Da Cjl = Clj gilt, setzen wir in der zweiten Summe Cjl = Clj und benennen dann j in k um. Das ist der übrigens der Grund, weshalb Cjk symmetrisch gewählt werden sollte. Wenn Cjk nicht symmetrisch ist, dann erhält man hier eine neue Matrix:

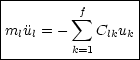
|-----------------| | f | |ml¨ul = - sum Clkuk| | k=1 | ------------------

Dies sind f Differentialgleichungen 2.Ordnung. Sie sind homogen, linear und haben konstante Koeffizienten. Leider sind sie aber miteinander gekoppelt.

[next] [prev] [prev-tail] [front] [up]