3 Hamiltonsche Formulierung der Mechanik

[next] [prev] [prev-tail] [tail] [up]

Kapitel 3
Hamiltonsche Formulierung der Mechanik

3.1 Integrale der Bewegung von Teilchen im Zentralfeld
3.2 „Blick über den Zaun“: Bedeutung von

v ec17EA und

Ziele:

Energie an 1.Stelle
Koordinate xqQ,
Geschwindigkeiten folgen aus der Koordinatentransformation. Koordinaten und Impulse werden mathematisch betrachtet.
Quantenmechanik leichter mit Hamiltonformel als mit Lagrangeformel

Hamiltonfunktion und Bewegungsgleichung
- Lagrangefunktion: $|-----------@L-----@L--| L(q, ˙q,t),p =---,f = --- | ------------@q˙----@q--|$
- Bewegungsgleichung: $|dp-----| |---= f | -dt-----|$
  Diese ist die Newton-Form der Lagrange-Bewegungsgleichung.
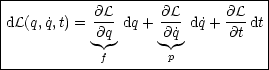
- Totales Differential: $|---------------------------------| | @L @L @L | |dL(q, ˙q,t) = @q dq+ -@˙q d˙q+ @t-dt| | | -------------f-------p------------$
  Hamiltonfunktion:
  $|------------------------------| H = pq˙- L als Funktion von q, p, t --------------------------------$
  Betrachten wir hier das totale Differential:
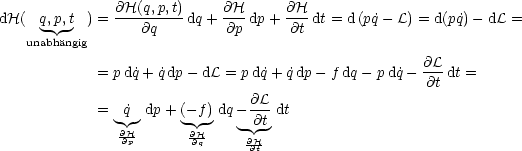  $dH( q,p,t ) = @H(q,p,t)dq + @H-dp+ @H-dt = d (pq˙-L) = d(p˙q)- dL = - - @q @p @t unabh¨angig = pdq˙+q˙dp- dL = pdq˙+ ˙qdp- f dq- pdq˙- @L-dt = @t = q˙ dp+ (- f)dq- @L-dt - - -@t @H@p @H@q @H- @t$ (3.1)
Wir erhalten 2 gekoppelte Differentialgleichungen:
$|-------------| | @H(p,q,t)-| |˙q = @p | --------------$

$|-----------------| | @H(p,q,t)| p˙= f = ----@q----| -------------------$

Dies sind die Hamiltonschen (kanonischen=unveränderlichen) Bewegungsgleichungen. Dabei handelt es sich um zwei gekoppelte Differentialgleichungen 1.Ordnung für p(t) und q(t).
Beispiel: Harmonischer Oszillator
$L(x, ˙x,t) = m-˙x2- D-x2 2 2$

$p = @L-= m ˙x @x˙$

$( ) 2m-˙x2 m- 2 D- 2 H = p˙x- L = 2 - 2 ˙x - 2 x$

$m D H = -2 ˙x2 + 2 x2$
Die Hamilton-Funktion entspricht im Falle des harmonischen Oszillators der Energie!
$|-------------------| |H(p,x) = p2-+ D-x2 | ----------2m----2---|$

$dx-= ˙x(t) = @H-= p- dt @p m$

$dp- @H- dt = ˙p(t) = - @x = -Dx$

Hamilton-Funktion und Bewegungsgleichung


	„Systemfunktion“		Bewegungsgleichungen


Lagrange	L = L(q,,t)	p = ,f =	= f
Hamilton	H := p -L		=
	H = H(p,q,t)		= -
			2 Differentialgleichungen 1.Ordnung
			(Kanonische Gleichungen)

\text{[math]}

Es gibt verschiedene Fachbegriffe, mit denen man den Impuls p bezeichnet:

Verallgemeinert
Generalisiert
Kanonisch
Kanonisch konjugiert
Konjugiert (zu q)

Zeitliche Änderung physikalischer Größen, Poisson-Klammer

Es sei eine physikalische Größe G = G(p,q,t) (Zustandsgröße) gegeben. Dann wird die Zustandsänderung längs der Bahnkurve dargestellt durch:

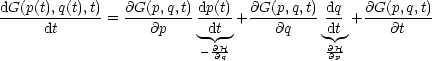
dG(p(t),q(t),t) @G(p,q,t) dp(t) @G(p, q,t) dq @G(p,q,t) ------------- = --------------+--------- -- + --------- dt @p dt- @q dt @t - @H@q @@Hp

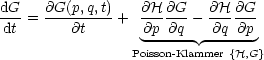
dG @G(p,q,t) @H @G @H @G dt-= ---@t----+ -@p-@q - @q-@p- ------ ------ Poisson-Klammer {H,G}

Wir notieren uns die Definition Poisson-Klammern (Reihenfolge: Landau-Lifschitz (und nicht Fließbach!)):

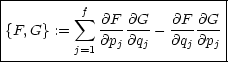
|---------f-----------------| |{F,G}:= sum -@F @G-- @F- @G-| | j=1@pj @qj @qj @pj| -----------------------------

Eigenschaften:

Antisymmetrie: ${F, G}= -{G,F }$
{F,C} = 0, wenn C unabhängig von p,q ist
Linearität: ${a F + a F ,G}= a {F ,G}+ a {F ,G} 1 1 2 2 1 1 2 2$
{F₁ ^. F₂,G} = F₁{F₂,G} + {F₁,G}F₂
Jacobi-Identität: ${F1,{F2,F3}}+ {F2,{F3,F1}}+ {F3{F1,F2}}= 0 f¨ur alle F1, F2, F3$
{p_j,q_k} = _jk,{p_j,q_k} = {q_j,p_k} = 0 für kanonische Variablen
{H,F} = 0
Daraus folgt, daß F = eine Erhaltungsgröße (Integral der Bewegung) ist, wenn F nicht explizit von t abhängt.
Differentiation nach p,q: $@F-(p,q,t)= {F,q} @p$
Algebraische Operation: $@F-(p,q,t) @q = -{F,p}$