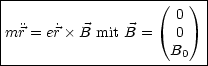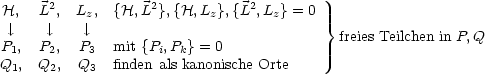
Aber wie findet man die Q’s?
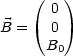
Die Newton-Gleichung lautet, wobei e die Ladung des Teilchens ist:
In Theoretischer Physik A hatten wir:
Und außerdem für die Zyklotron-Frequenz:
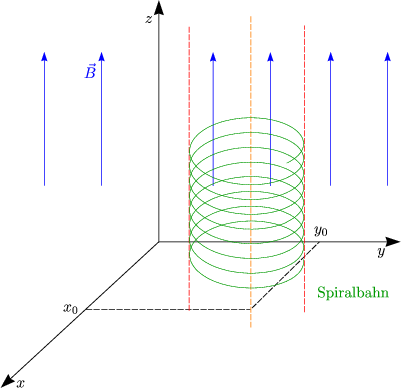
Dies ist nur dann ein Integral der Bewegung, wenn die Spiralachse der z-Achse entspricht, das heißt wenn x0,y0 = 0 gilt!
Die Lagrange-Funktion lautet:
Wir haben beispielsweise:
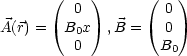
Dann ist ![]() (
(![]() ) das sogenannte „Vektorpotential“. Wir notieren uns außerdem
die Hamilton-Funktion:
) das sogenannte „Vektorpotential“. Wir notieren uns außerdem
die Hamilton-Funktion:
![]() und
und ![]() sind kanonische Variablen.
sind kanonische Variablen.
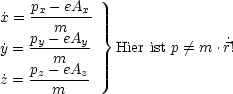
Für den kinetischen Impuls gilt jedoch:
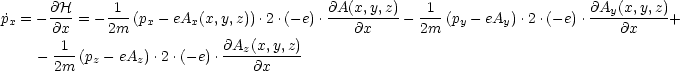 | (3.2) |
![[ ] [ ]
d- px--eAx- ˙px -e-d d-
mx¨ = m dt m = m m - m dtAx = p˙x - edtAx =
px- eAx @Ax py- eAy @Ay pz - eAz @Az d
= ---m----.(+e).-@x- + ---m----.(+e).-@x-+ ---m----.(+e) .@x---edtAx(x,y,z)
----------------------------- -----------------------------
˙px](th430x.gif) | (3.3) |
Nach Newton erhalten wir: