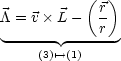2 Zweikrper-System mit zentraler Wechselwirkung

Kapitel 2
Zweikörper-System mit zentraler Wechselwirkung

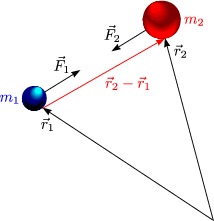
m₁

₁ =

₁ = f(r)

m₂

₂ =

₂ = -

₁

r = r1- r2

m1m2-- dU(r) f(r) = - G r2 = - dr

m1m2 d U(r) = - G--r--= - r

Das Ziel ist es, die Bewegungsgleichungen zu lösen. Leider ist kein Ansatz für beliebige U(r) möglich.

2 Körper, 3 Dimensionen 2 ^. 3 = 6 Freiheitsgrade
2f - 1 = 12 - 1 = 11 unabhängige Integrale der Bewegung, die nicht von t abhängen

Impuls (3 Integrale der Bewegung): $˙ P = p1 + p2 = m1v1 + m2v2 = (m1 + m2)R$
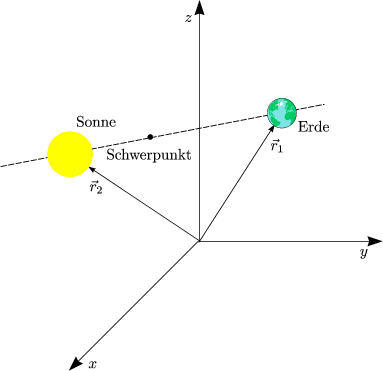
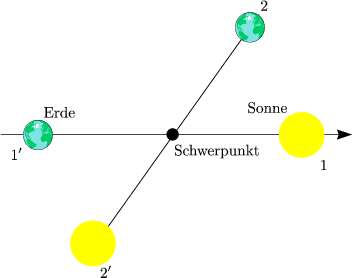
Der Gesamtimpuls ergibt sich aus Relativ- und Schwerpunktskoordinaten:
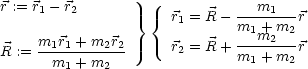
$r := r1 - r2 } { r = R - ---m1---r 1 m1 +m m2 R := m1r1-+-m2r2 r2 = R +----2---r m1 + m2 m1 + m2$

$(m1 + m2)R˙= p --- --- M$
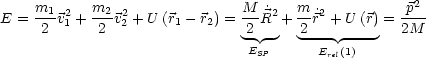
Energie (1 Integral der Bewegung): $m1-2 m2- 2 M--˙2 m-˙2 p2-- E = 2 v1 + 2 v2 + U (r1- r2) = 2 R + 2r--+-U (r)= 2M ESP Erel(1)$
Drehung (3 Integrale der Bewegung): $L = r1× p1 + r2× p2$
Das ganze verhält sich additiv:
$L = R-× P + r× p LSP Lrel$
Getrennt erhalten wir 5 Integrale der Bewegung. _SP = × besteht aus 3 Komponenten. Da _SP, sind aber nur 2 Komponenten von _SP unabhängig. Damit wären nun 9 von 11 Integralen der Bewegung gefunden.

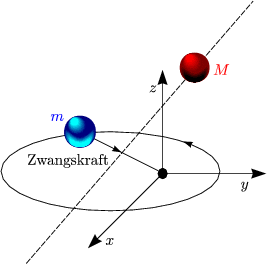
Freies Teilchen (Schwerpunkt)

R = R0 + V0t mit R0,V0 beliebig

Kepler-Ellipse fur U(r) = - a ¨ r

M,m sind Teilchen, aber keine Körper; haben auch keine Wechselwirkung.

Relativ: Teilchen in Zentralkraftfeld

Lrel ist erhalten, Bewegung in einer Ebene

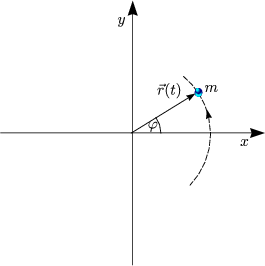
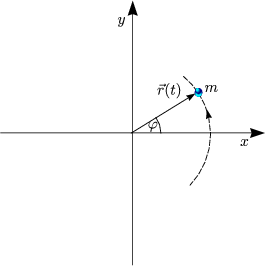
Wir führen Polarkoordinaten ein:

x = rcosf,y = rsin f,(z = 0)


m = f(r)	E_rel = ² + U erhalten


Differentialgleichung 2.Ordnung	Differentialgleichung 1.Ordnung.
Separation der Variablen r	Separation der Variablen t

m₁

₁ = -

m₂

₂ = +

₁ = -gradV (

₁,

₂) = -

V (

₁,

₂) = U(|

₁ -

₂|)

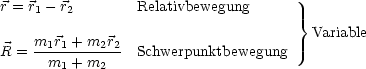
r = r - r Relativbewegung 1 2 } m r + m r Variable R = -1-1----22- Schwerpunktbewegung m1 + m2

|-------| |M ¨r = 0|freies Teilchen der Masse M = m +m -------- 1 2

|------------(--)-| | ¨ dU-(r) r | m1-.m2-- ˙ m r = - dr r Teilchen im Potential U(r),m = m1 + m2,p = m r ------------------

Hierbei handelt es sich nun um ungekoppelte Gleichungen! Wir nutzen die Integrale der Bewegung aus:

Impuls (3): $P = m1r˙1 + m2 ˙r2$
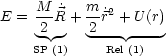
Gesamtenergie (2): $M m E = ---˙R+ -r˙2 + U(r) 2 - 2--- ---- SP (1) Rel (1)$
Gesamte Drehung (4): $L = R-× P + r× p (3)'-->(1) (3)$
10.Integral der Bewegung:
Es handelt sich um den Lenz-Runge-Vektor für U(R) = - gilt:
$( ) /\ = v × L - r r ----(3)'-->(1)----$
11.Integral der Bewegung: ?