2.3 Keplerproblem

r = r(f) =------p-------- 1+ ecos(f- f0)

Man eliminiert nun dt durch d, indem man die Zeit durch den Drehimpuls ausdrückt:

df Lz = mr2--- dt

integral integral mLrz2 df = -- V~ -2-----------dr = f- f0 ± m [E- Veff (r)]

Mit quadratischer Ergänzung folgt dann:

( ) ( ) 2- 2E- -a- 2 Lz-- -a- 2 m [E - Veff] = m + Lz - 2mr - Lz -----j2----- -----q2-----

Zähler ist die Ableitung des Radikanten der Wurzel im Nenner!

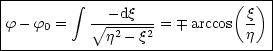
|-------- integral ------------------(--)-| |f- f0 = V~ --dq-- = ± arccos q- | -------------j2--q2------------j---

Wir bilden die Umkehrfunktion und drücken r durch r() aus:

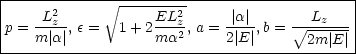
|-------------------------------------------| | L2 V~ ----EL2-- |a | L | |p =--z-, e = 1+ 2---z2, a =----,b = V~ -z---| ----m-|a-|----------ma-------2|E|------2m-|E-|-

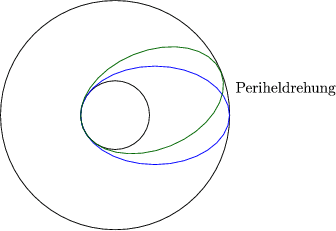
Diese Größen sind also nur von E abhängig!

U(r) = - a-+ bn n /= 1 r r