1.5 Symmetrien und Erhaltungsgren

1.5 Symmetrien und Erhaltungsgrößen

Eine Symmetrie ist eine Transformation der Koordinaten und Zeit, die eine charakteristische Größe invariant läßt (Bewegungsgleichungen S[q(t)] L(q,,t)). L(q,,t) ist invariant gegen tt + t₀, d.h. L hängt nicht explizit von t ab. Dies nennt man „Homogenität der Zeit“.

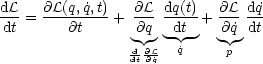
dL-= @L(q, ˙q,t)-+ @L dq(t)+ @L- d˙q dt @t @q dt- @q˙ dt d-@L- ˙q p dt@˙q

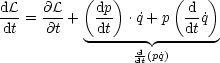
( ) ( ) dL- @L- dp- d- dt = @t + dt .˙q+ p dt ˙q ------d ------- dt(pq˙)

d @L dt (pq˙-L) + @t-= 0

Es handelt sich um ein Integral der Bewegung, also eine Erhaltungsgröße. Falls = 0 ist, gilt p -L = const.

Bemerkung:

Eigentlich ist „Homogenität der Zeit“ die Invarianz des mechanischen Systems ___________________ gegenüber Zeittranslationen. Somit ist die Invarianz der Lagrangegleichung und nicht die Invarianz der Lagrangefunktion entscheidend!

Die Invarianz der Lagrangegleichung folgt aus der Invarianzbedingung des erweiterten Noethertheorems. Im Falle der Zeittranslation folgt die Invarianz der Lagrangegleichung auch aus der Invarianz der Lagrangefunktion. Die Invarianzbedingung ist also allgemeiner.

Symmetrie:

Darunter versteht man die Invarianz der Lagrangefunktion (und damit der Bewegungsgleichung) unter einer (einparametrigen) Transformation von Raum und Zeit. Aus der Gleichheit der Lagrangefunktion folgt die Gleichheit der Bewegungsgleichungen. Die Umkehrung gilt allerdings im allgemeinen nicht.

Invarianz gegen Zeitverschiebung tt + t₀ („Homogenität der Zeit“) $L(q,q˙,t) '--> L(q,q˙)$
Daraus ergibt sich:
$d-L(q(t), ˙q(t)) auf Bahnkurve q(t) dt$
Wir folgern als Erhaltungsgröße:
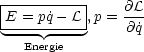
$|E-=-p˙q--L-,p = @L -----------| @˙q Energie$
Verschiebung des Koordinatensystems $ra '--> ra + e (kleine Verschiebung)$

$va '--> va$
Der Index a bezeichnet die Nummer des Teilchens.
$L(r1,...,rN ,v1,...,vN-,t) ist invariant gegen e. kein Einfluß$
Wir führen nun eine Kurzbezeichnung ein, die eigentlich verboten ist, nämlich die Differentiation nach einem Vektor. Also definieren wir:
$|---------------------------| |@L (@L @L @L ) | |@r-:= @x-,@y,-@z = gradrL| -----------------------------$
Dies hat folgende Konsequenzen für die Lagrange-Gleichung:
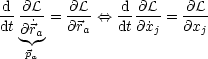
$d- @L-= @L-<==> d-@L--= @L-- dt @˙ra @ra dt@x˙j @xj pa$

$' df = f (x) dx e$

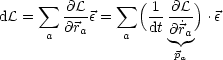
$dL = sum -@L e = sum (1 @L-).e a @ra a dt @˙ra p a$

$( ) dL = -d sum p .e=!0 soll f¨ur beliebiges e gelten, also: dt a a$

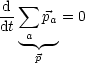
$d sum -- pa = 0 dt a - p$
Wir nennen Impuls (generalisierter Impuls), wobei als Nebenbedingung gelten soll, daß dieser sowohl additiv als auch mengenartig ist.
Invarianz gegen Drehungen des Koordinatensystems

$|dr| = |r|.|df |$
- Drehung um beliebige Achse dr
- Drehung um Winkel |d|
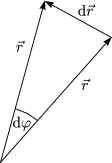
Für kleine Drehungen gilt:
$|-----------| -dr-=-df×-r-|$
Demnach erhalten wir für das Teilchen:
$dra = df× ra$

$dv = df× v p .(df × v) = df.(v × p )+ Produktregel a a a a a a$

$dL = sum [@L-.dr + -@L .dv ] a @ra a @va a dp pa dta$

$sum sum dL = df . -d(ra× pa)=! 0 A df ==> L = ra ×pa ist erhalten. a dt a$

Die drei genannten Fälle sind Spezialfälle des sogenannten Noether-Theorems: Invarianz der Lagrangefunktion gegen Raum-Zeit-Transformation (einparametrig, infinitesimal) Dies findet man speziell im Fließbach unter dem Kapitel „Erhaltungsgrößen“.

[prev] [prev-tail] [front] [up]