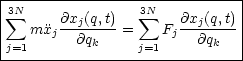
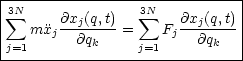
Eingesetzt in die Differentialgleichung ergibt:
Die Masse fällt heraus, da schwere und träge Masse gleich sind.
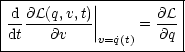
Nach dem Standard-Modell gilt:
Für die Wirkung erhalten wir:
![|-------------------------|
| integral tb |
|S[q(t)] = L (q(t),v(t),t) dt|
| ta |
--------------------------](th64x.gif)
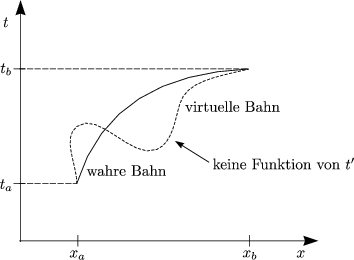
Die Wirkung S nimmt ein Minimum für die wahre Bahn (feste Anfangs- und Endpunkte) an.
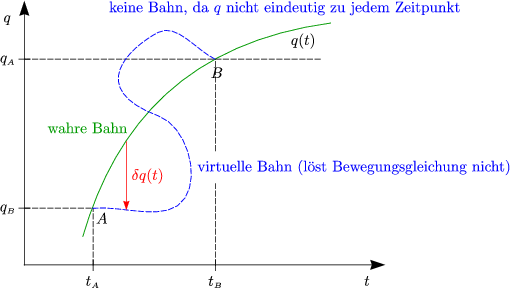
S![]() sei für q(t) stationär (Ableitung von S). Oft ist S
sei für q(t) stationär (Ableitung von S). Oft ist S![]() minimal
für q = q(t), das heißt S
minimal
für q = q(t), das heißt S![]() < S
< S![]() für alle q(t), die A und B
verbinden.
für alle q(t), die A und B
verbinden.
Die Natur liebt Extremalprinzipien wie beispielsweise das Fermat’sche Prinzip.
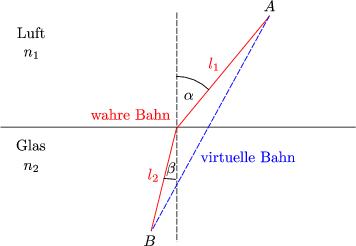
Wenn die Zeit minimal wird, ist das Brechungsgesetz erfüllt.
(Meier ![]() M eier)
M eier)
Aus y = f(x) folge y = y(x).
![- integral tb[@L(q, ˙q,t) @L(q, ˙q,t) ]
S[q(t)] = S [q(t)]+ e --------j(t) + --------˙j(t) dt+ O(e2)
ta @q @˙q](th82x.gif)
Unser Ziel ist die Stationarität von S[q(t)]. Dies erfordert S'(![]() ) = 0, womit also
gelten muß:
) = 0, womit also
gelten muß:
![]() (T) sei beliebig! Aus
(T) sei beliebig! Aus ![]() (t) folgt dann
(t) folgt dann ![]() (t) durch partielle Integration:
(t) durch partielle Integration:
![integral @L @L ||tb t integral b[d @L(q,q˙,t)]
-@˙q ˙j(t)dt = @-˙q .j(t)|| - dt---@-˙q--- .j(t)dt
---- --ta ta
=0](th85x.gif)
![t integral b[ ]
S [q(t)] = S [q(t)]+e @L-- -d@L- j(t)dt+ ...
@q dt @˙q
ta---------- -----------
!=0 f¨ur alle j(t)](th86x.gif)
Der Integrand muß 0 sein, da ![]() (t) eine beliebige Funktion ist.
(t) eine beliebige Funktion ist.
Dies ist gerade die Lagrange-Gleichung 2.Art.
Damit erhalten wir folgende Bewegungsgleichung:
Die Voraussetzung ist, daß alle qk’s unabhängig sind, daß als keine Zwangsbedingungen zwischen den qk’s herrschen.
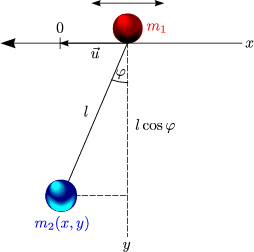
Wir betrachten ein ebenes mathematisches Pendel mit frei gleitendem Aufhängepunkt mit Masse. Es gibt dann die Freiheitsgrade 1(m1) + 1(m2). Wir führen generalisierte Koordinaten ein:
Wir haben dann folgende Lagrange-Funktion:
Wir differenzieren die Koordinaten nach der Zeit:
Durch Einsetzen in die Lagrange-Funktion erhalten wir:
Für u gilt:
Des weiteren folgt für ![]() :
:
Es handelt sich um eine Erhaltungsgröße!
Für m1![]()
![]() erhalten wir das übliche mathematische Pendel:
erhalten wir das übliche mathematische Pendel:
Mit m1![]() 0 haben wir folgendes Resultat:
0 haben wir folgendes Resultat:
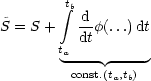
![]() (q,t) heißt „Eichfunktion“.
(q,t) heißt „Eichfunktion“.
Ziel der Lagrangetheorie: Wähle (wenn möglich) zyklische generalisierte Koordinaten!
pk ist der verallgemeinerte Impuls, fk die verallgemeinerte Kraft.
Wenn das Relativitätsprinzip für die Lagrange-Funktion gelten soll, muß folgendes erfüllt sein:
f sei hierbei eine unbekannte Funktion, die vom Ort ![]() und der Zeit t abhängt.
Allgemein gilt nun für deren Zeitableitung:
und der Zeit t abhängt.
Allgemein gilt nun für deren Zeitableitung:
Wir betrachten nun die Taylor-Entwicklung von L:
![( ) [ ]
~L v2 + 2vv + v2 = L(v2)+ -@L .e+ ...= L (v2)+ -@L--.2v v+ ...
--0 --0 @v2 -@(v2) ---0
kleine Gr¨oß e e darf nicht von
v abh¨angen](th143x.gif)
Wegen ![]() f(
f(![]() ,t) = (gradf) .
,t) = (gradf) .![]() +
+ ![]() muß
muß ![]() 2
2![]() 0
0![]() linear in
linear in ![]() sein und
damit
sein und
damit ![]() . 2
. 2![]() 0 unabhängig von
0 unabhängig von ![]() . Damit hängt L linear von
. Damit hängt L linear von ![]() 2
ab:
2
ab:

In der Quantenmechanik hat man eine sogenannte Wellenfunktion:
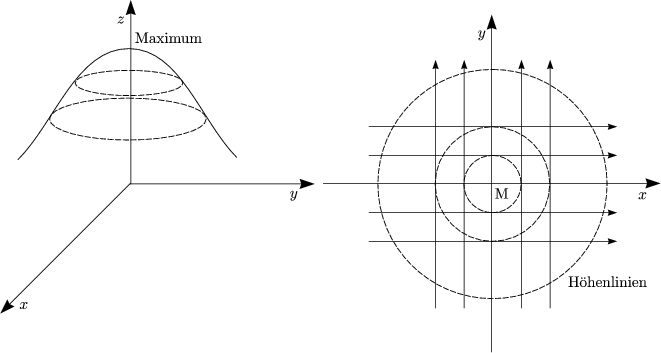
Aus f'(x) = 0 folgt durch Auflösen x0 als Extremwert. Es handelt sich dann um ein Minimum, falls f''(x0) > 0 bzw. um ein Maximum, falls f''(x0) < 0 ist. Im Falle f''(x0) = 0 haben wir einen eventuellen Wendepunkt.
Für die Extremwerte, muß folgendes gelten:

x0, y0 heißt dann Extremalpunkt (stationärer Punkt) von f(x,y). Wir
untersuchen F(s) = f(x0 + scos![]() ,y0 + ssin
,y0 + ssin![]() ) mit festem
) mit festem ![]() :
:

Andernfalls handelt es sich um einen Sattelpunkt.
fxx, fyy, fxy sei bei (x0,y0) bekannt. fxx . fyy - fxy2 > 0 gilt sowohl für
Minimum als auch Maximum!
Wenn die Matrix ![]() indefinit ist, handelt es sich um einen
Sattelpunkt. Bei Semi-Definitheit sind weitere Untersuchungen notwendig!
indefinit ist, handelt es sich um einen
Sattelpunkt. Bei Semi-Definitheit sind weitere Untersuchungen notwendig!

Viel einfacher ist folgende Betrachtung:
Durch Differentiation nach m erhalten wir 2fxy + 2m0fxy![]() 0. Anschließend setzen
wir m0 = -
0. Anschließend setzen
wir m0 = -![]() in F''(0) ein und fordern F''(0) > 0. Für N unabhängige Variablen
f(x1, x2, ..., xN) findet man die stationären Punkte durch:
in F''(0) ein und fordern F''(0) > 0. Für N unabhängige Variablen
f(x1, x2, ..., xN) findet man die stationären Punkte durch:
Funktion x(t) als „Variable“
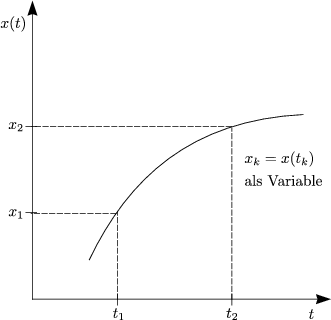
Funktion f(x1, ..., xN) ![]() f[x(t)] (Funktional)
f[x(t)] (Funktional)
![t
integral b d
f [x(t)] = L(x(t), ˙x(t),t)dt mit ˙x(t) = dtx(t)
ta](th196x.gif)
Die stationären „Punkte“ findet man dann durch Lösen von:
Es sei z = f(x,y) mit g(x,y) = 0 als Nebenbedingung gegeben. Es gibt zwei Arten von Nebenbedingungen:
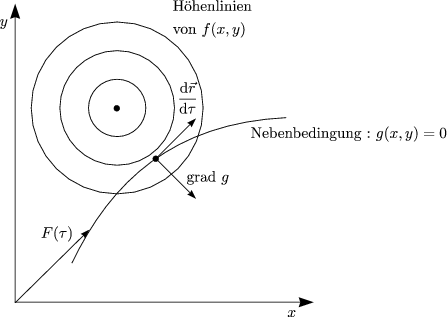
Also ist grad(f) =const. . grad(g) für stationäre Punkte, d.h. man findet die stationären Punkte mit:
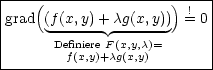
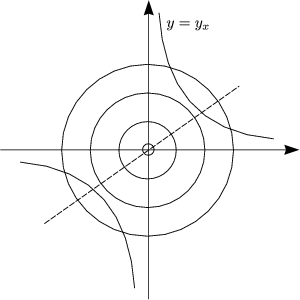
Mit x = y, was man aus den ersten beiden Gleichungen erhält, folgt durch Einsetzen
in F![]() :
:
Daraus erhält man dann folgende Lösungen des Problems (Variation mit holomorpher Nebenbedingung):
Nun wieder zurück zur Physik! Betrachten wir die Langrange-Funktion:
Wir haben die Nebenbedingung g(x,y,z,t) = g(![]() ,t) = 0.
,t) = 0.
![integral tb integral
˙
S[r(t)] = L(r,r,t)dt + c(t)g(x(t),y(t),z(t),t) dt
ta](th221x.gif)
Für die Extrema folgt dann:
Dies ist die Lagrange-Gleichung 1.Art (Varitation mit isoperimetrischer Nebenbedingung).

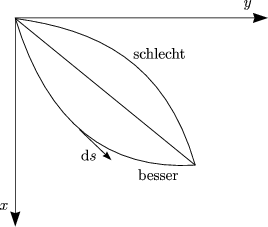
Wir suchen die kürzeste Rutschzeit:
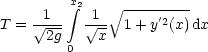
Nun kommen wir zur Berechnung:
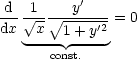
Wir lösen nach y' auf und erhalten:
Kettenlinie ist Kosinushyperbolikus
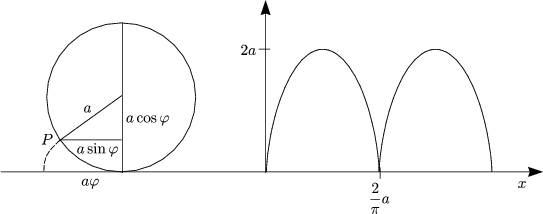
a folgt aus y(xc) = yc. y(x) ist eine sogenannte Zykloide. Wir können diese Gleichung auch in Parameterdarstellung folgendermaßen schreiben:
In der Mathematik vertauscht man x mit y (x![]() y):
y):