1.3 Lagrange-Mechanik

Ziele:Zwangsbedingungen ==> Lagrange-Funktion -----

Zwangsbedingungen und Zwangskräfte
$g(x,y) = x2 + y2- l2 = 0$

Newton:
$|--¨------------------| -m-r =-Fges =-FGr-+-FZw$
_Zist eine Zwangskraft, die für g(x,y) = 0 gilt. Die Zwangskraft _Z steht senkrecht auf g(,t) = 0. Also gilt:
$|-----------------| |F = c.grad g(r,t)| --Z----------------$
Für unser Pendel erhalten wir:
$g = x2 + y2- l2$

$grad g = (2x,2y,0)$
ist der Lagrange-Parameter. Damit gilt für N Teilchen (j = 1, 2, ..., N) und R Zwangsbedingungen g = 0 die Lagrange-Gleichung 1.Art.
1.3.1 Lagrange-Gleichung 1.Art
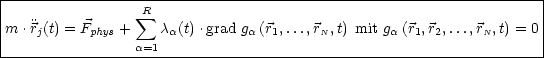
$|-------------------------------------------------------------------| | sum R | |m .¨rj(t) = Fphys + ca(t).grad ga (r1,...,rN,t) mit ga (r1,r2,...,rN,t) = 0 -----------------a=1-------------------------------------------------$
Es handelt sich um 3N + R Gleichungen für _j(t), (t).
Beispiel: Mathematisches Pendel
- m = 0 + (t) ^. 2x
- mÿ = -mg + (t) ^. 2y
- x² + y² - l² = 0
Diese Differentialgleichungen sind leider nicht analytisch zu lösen. Es wäre besser, sogenannte generalisierte Koordinaten einzuführen:
$qk,k = 1,2,...,3N - R = f$
f ist die Zahl der Freiheitsgrade.
$r1,r2,...,rN = x = {xj}f¨ur j = 1,2,...,3N$

$x = x (q ,q ,...,q ,t) j j 1 2 f$
Für das mathematische Pendel gilt:
$x1 =_ x = l.sin f$

$x2 =_ y = l.cosf$

$Generalisierte Koordinate: q =_ f$
Die Zwangsbedingung ist identisch erfüllt:
$2 2 2 g(x,y) = x-+-y---l = 0 =_ 0$

Strategie:

Wähle q_k so, daß die Zwangsbedingungen identisch erfüllt sind, d.h., daß die q_k unabhängig voneinander sind. Die Lagrangegleichungen werden so umgeformt, daß sie besser handhabbar sind. Man will also die Zwangskräfte „loswerden“!
$sum R mx¨j(t) = Fj + ca(t)@ga(x,t)- a=1 @xj$

$@x (q,t) 3 sum N Wir multiplizieren die Gleichung mit--j---- und bilden . @qk j=1$

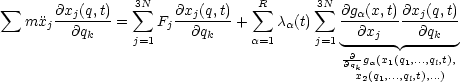
$sum @x (q,t) 3 sum N @x (q,t) sum R 3 sum N @g (x,t) @x (q,t) mx¨j --j---- = Fj--j---- + ca(t) --a-------j---- @qk j=1 @qk a=1 j=1 -@xj-- --@qk- @@qkga(x1(q1,...,ql,t), x2(q1,...,ql,t),...)$
Sofern die Zwangsbedingungen identisch erfüllt sind, gilt:
$-@- @qkga(x1(q1,...,ql,t),x2(q1,...,ql,t),...) =_ 0$
zeigt in Richtung der Zwangskraft und ist senkrecht zur q_k-Koordinatenlinie. Projektion auf die Tangential-Fläche der Nebenbedingung (genauer: auf die q_k-Koordinatenlinie)
[next] [prev] [prev-tail] [front] [up]

1.3 Lagrange-Mechanik

Newton:

1.3.1 Lagrange-Gleichung 1.Art

Beispiel: Mathematisches Pendel

Strategie: