[next] [prev] [prev-tail] [tail] [up]

1.2 Bezugssysteme und Relativitätsprinzip

Bezugssystem: „Koordinatensystem+Uhren“
PIC

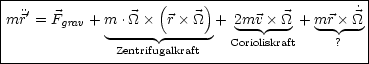
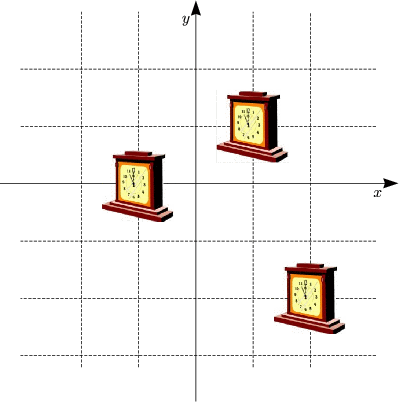
Ein Koordinatensystem ist ein starres Gerüst von Maßstäben.

Inertial-System:
Wir nehmen an, daß ein kräftefreies Teilchen eine konstante Geschwindigkeit hat, also v=const. gilt. Wenn dies nicht gilt, gibt es zwei Möglichkeiten:
  1. Es ist doch eine Kraft vorhanden.
  2. Das System ist nicht inertial.

1.2.1 Klasse von Inertialsystemen

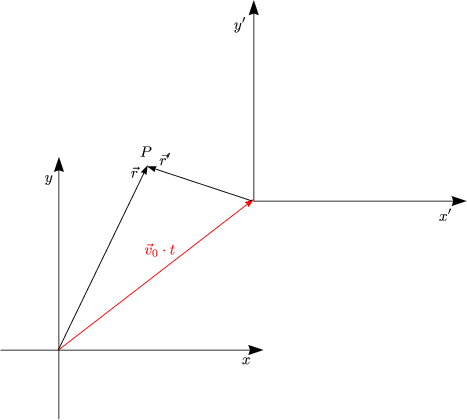
K sei Inertialsystem. Dann auch K' mit:

PIC

|'---------------| r-=-r--v0-.t+-R0-|

|'----------------| t-=-t-(absolute-Zeit)-

R0,v0 = const.

Hierbei handelt es sich um die sogenannte Galilei-Transformation.

1.2.2 Relativitätsprinzip

Naturgesetze haben in allen Inertialsystemen dieselbe Form. Beispielsweise lautet die Beziehung zwischen Energie und Geschwindigkeit für ein freies Teilchen:

E = m-v2 <--> E'= m-v'2 2 2

d2r(t) Bewegungsgleichung: m -dt2--= F (r) ------ ------ invariant gegen Galilei

1.2.3 Exkursion: Lorentz-Kraft

( ) F = q E + v × B

1.2.4 Einstein’sches Relativitätsprinzip

Relativitätsprinzip plus Annahme, daß Lichtgeschwindigkeit in allen Inertialsystemen gleich (Galilei ==> Lorentztransformation)

Nichtinertiale Bezugssysteme
mr¨/= F (=Kraft aus Inertialsystem)

! mr¨= Fges = Fgrav + Fschein

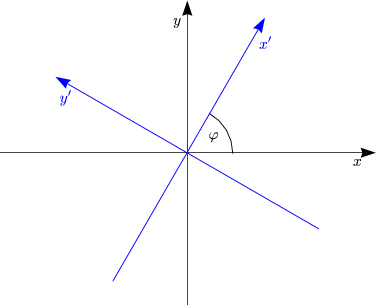
Beispielsweise ist ein rotierendes Bezugssystem nicht inertial.

PIC

f = _O_ .t

|-------------------(-----)-------------------| |m¨r'= Fgrav + m ._O_ × r× _O_ + 2mv × _O_ + mr × _O_˙| | ------ ------ Corioliskraft --?-- | ---------------Zentrifugalkraft----------------------

Äquivalenzprinzip:
Gravitationsfeld /\ = beschleunigtes Bezugssystem

LOKAL

[next] [prev] [prev-tail] [front] [up]