10 Elektrodynamik in kontinuierlichen Medien

[prev] [prev-tail] [tail] [up]

Kapitel 10
Elektrodynamik in kontinuierlichen Medien

Elektrostatik:
Wir betrachten Moleküle in der Größenordnung von 10^-10 m = 1Å. Bei sichtbarem Licht beträgt die Wellenlänge = 3,8 - 7,5 ^. 10^-7 m. Selbst bei Ausbreitung und zum Teil bei Streuung wird über viele Moleküle gemittelt. Mehrdimensionale Felder und Ladungsverteilungen sind räumlich und zeitlich veränderlich. Relevant sind somit gemittelte Größen. , , , seien die mikroskopischen Größen (verschoben mit -Polarisierbarkeit). , , seien die mehrdimensionalen Größen., wobei gilt:
$integral E(x) =-1-- djE(x,j) = <E(x)> DV DV$
V ist hierbei ein geeignet gewähltes Volumen. Wir mittel somit über zeitlich veränderliche Größen:
$x+ integral DL -1- r(x) = <j(x)> = DL dx j(x) x$
Es gilt:
$< > -d-E(x,t) = d-,e(x,t) dxi dx$
Ähnlich gilt:
$< > @-E(x,t) = @-e(x,t) = 0 f¨ur Statik @t @t$
Wir betrachten nun den Beitrag der Ladungsdichte _j eines Moleküls mit Index j zum Feld am Punkt . Dazu verwenden wir den Gaußschen Satz:

$x /\ = Beobachter$

$xj /\ = Schwerpunktskorrdinaten des Molek¨uls$

$/\ x'= Relative Koordinate$

$|x'|< O(1 ºA) < |x - xj- x'|$
Mit dem Gaußschen Satz erhalten wir für das mehrdimensionale Feld:
$1 integral jj(x') ej(x) = - 4pe- \~/ |x---x---x'|d3x' 0 Molek¨ulj j$
Mit der Taylor-Entwicklung folgt:
$1 1 ( 1 ) |x---x---x'|-= |x---x-|+ \~/ j |x---x-| .x' j j j$

$( ( ) ) ej(x) = ---1- \~/ --ej---+ \~/ ---1--- .pj 4pe0 |x - xj| |x- xj|$
Mit der Gesamtladung e_j:
$integral ej = dx'jj(x')$
Und dem Dipolmoment:
$integral ' ' ' pj = dx jj(x ).x$
Für den Beitrag aller Moleküle folgt durch Summation:
$rmol(x'') = sum ejd(x''- xj) j$

$TT (x) = sum p d(x''- x ) mol j j j$
= _j_j wird nun umgeschrieben in ein Integral:
$-------------------------------------------------- | 1 integral [r(x'') ( 1 )] | |e(x) = ----- \~/ dx'' ------'' + TT(x''). \~/ -----'' | ---------4pe0--------|x--x-|------------|x--x-|---|$
() ist immer noch schnell veränderlich, da ('') schnell veränderlich ist.

Wir führen eine Mittelung durch und betrachten somit den Beitrag von _mol('').
$e = e + e r TT$

$integral integral '' <er(x)> = -- \~/ - dq dx''-rmol(x-)-- 4pe0 |x - x''+ q| DV um x$
Wir führen eine Variablensubstitution durch:
$x'''--> x'= x''-q$
Die Mittelung verläuft über :
$integral -1-- dqr(x'+ q) =--1- sum e DV DV DV j DV$

$integral E (x) = <e (x)>> = -- \~/ - dx'N-(x')emol(x') r r 4pe0 |x - x'|$

$N (x')= /\ Dichte der Molekule ¨$

$' /\ emol(x )= Mittlere Ladung (gemittelt¨ uber DV )$

$integral -1-- d3q TTmol(x'+ q) = N(x')pmol(x') DV DV$

$integral ( ) ETT(x) = <eTT(x)> = -- \~/ d3x'N (x')pmol(x'). \ ~/ '-1---- 4pe0 |x - x'|$
_mol(') ist das mittlere Dipolmoment eines Moleküls am Punkt '. Wir definieren nun die mittlere Ladungsdichte und die Dipolmoment-Dichte (makroskopische elektrische Polarisation):
$r(x) =_ N (x).emol(x)$

$p(x) =_ N (x).pmol(x)$

$E = Er + ETT$

$integral ( r(x') 1 ) 4pe0E(x) = - \~/ dx' |x--x'|+ p(x'). \~/ '|x--x'|$
Beachte:
$' 1 2 1 ' - \~/ \ ~/ |x--x'|= \~/ |x---x'| = -4pd(x- x )$

$( ) integral ' 4p e0E(x) + p(x) = - \~/ dx'-r(x)-- |x - x'|$
Definiere () = ₀() + () als „elektrische Verschiebungsdichte“. Damit gilt dann:
$|---------1--- integral ----r(x')--| |D(x) = ---- \~/ dx'-----'-| ---------4p--------|x--x-||$
Außerdem gilt:
$|---------| \~/ D-=-r(x)-$

$|--------------------------| \~/ -×-E-=-0-in-der Elektrostatik$

Experimentelle Information:
Für langsam veränderliche, nicht extrem starke elektrische Felder hängen und linear zusammen. $pi(x) = aijEj(x)$
a_ij ist im allgemeinen ein Tensor. In einem isotropen Medium ist a_ij ~ _ij:
$p(x) = e0xE(x)$
ist eine Materialkonstante, nämlich die sogenannte Suszeptibilität. Diese gibt an, wie gut sich ein Medium polarisieren läßt.
$D = e0eE mit e = 1+ x$

Beispiel:

Material
Glas 4
Paraffin 2,8
Wasser 82

$|----------| | -1- | \~/ E = e0er | ------------$
Wobei die freie gemittelte Ladung beschreibt. Die Felder sind reduziert um den Faktor . Die Kapazität eines gefüllten Kondensators ist um den Faktor erhöht.
Randwertprobleme:
Unser Ziel ist, zu zeigen, daß die Komponente parallel zur Oberfläche stetig ist.

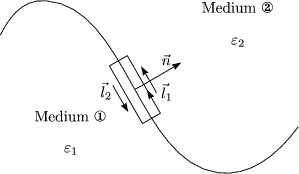
Wir verwenden den Stokesschen Satz:
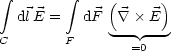
$integral integral ( ) dlE = dF \~/ × E --- --- C F =0$
Somit folgt nach Durchlaufen des Weges:
$0 = E1l1 + E2l2 mit l1 = -l2 = l$

$( ) E1 - E2 l = 0$
Damit ist gezeigt, daß die Komponente von || stetig ist. Mit der Flächennormalen gilt dann:
$|(-------)--------| | E1 - E2 × n = 0| ------------------|$
Für gilt:
$\~/ D = r$
Wir betrachten wieder die Grenzschicht:

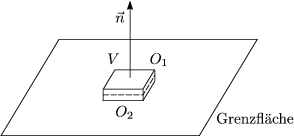
Nun gilt mittels der Maxwell-Gleichungen:
$integral integral \~/ D = r(x)dx V V$
Mit dem Gaußschen Satz resultiert:
$integral dF D = sO1 O$
Lassen wir die Dicke des Quaders gegen Null gehen, so gilt:
$O = O1 + O2 +kleine Randterme$

$( ) D1 - D2 .n .O1 = sO1$

$( ) D1 - D2 .n = s$
Falls keine Oberflächenladungen (makroskopischer freier Beitrag) vorliegen, gilt:
$|---------------| ( ) | --D1--D2--.n-=-0-$
Einfache Beispiele:
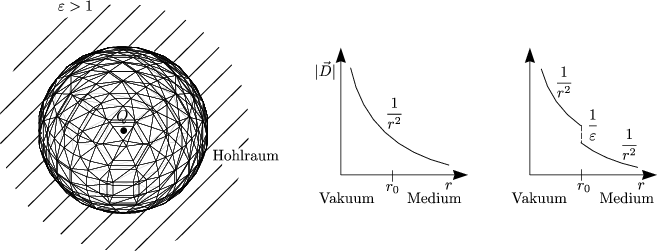
- Ladung Q im Hohlraum ( = 1), der von einem Dielektrikum ( > 1) umgeben ist:
- 2 leitende, entgegengesetzt geladene Kugeln, von 2 Dielektrika getrennt:
  
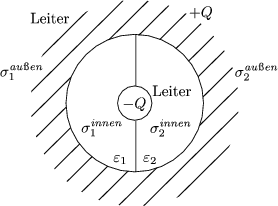
  Das Potential muß auf innerer und äußerer Kugel jeweils gleich sein. Man erhält die Potentialdifferenz durch Integration über das elektrische Feld von innen nach außen:
  $au integral ßen au integral ßen DU = - E1 dl1 = E2 dl2 innen innen$
  Da 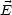₁ und 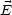₂ wie 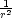abfallen und außerdem die beiden Integrale gleich sind, dann folgt daraus, daß auch E₁ und E₂ gleich sind.
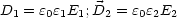
  $D1 = e0e1E1; D2 = e0e2E2$
  Damit ergibt sich folgendes Verhältnis:
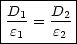
  $|---------| |D1- D2-| --e1-=--e2-|$
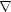
  Wegen 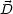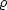$\~/$ = gilt folgender Zusammenhang zwischen der Flächenladungsdichte:
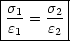
  $|s----s-| |-1= -2| -e1---e2-$
  Die Ladungen sind also nicht gleichmäßig verteilt. Je höher die Polarisierbarkeit an einer Stelle ist, umso mehr Ladung wird man an dieser Stelle antreffen. Dies gilt sowohl auf der Innen- (r) als auch auf der Außenkugel (R).
  $( ) 4pr2 2s2 e1 2 e1 +-e2 Q = 2 (s1 + s2) = 4pr 2 e2 + 1 = 4pr s2 2e2$
  
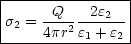
  $|-----Q----2e---| |s2 =---2 ---2--| -----4pr--e1-+-e2-$
  
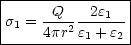
  $|---------------| | Q 2e1 | |s1 = 4pr2 e1-+-e2 -----------------$
  Somit gilt:
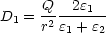
  $Q 2e D1 = 2----1-- r e1 + e2$
  
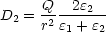
  $Q 2e2 D2 = r2-e-+-e- 1 2$
  Die Beträge der -Felder sind gleich:
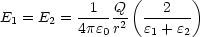
  $1 Q ( 2 ) E1 = E2 = 4pe-r2 e--+e- 0 1 2$
- In konstantem elektrische Feld wird eine Kugel mit Radius a und Dielektrizitätskonstante gebracht:
  
  Für das Potential gilt mit der Entwicklung in Kugelflächenfunktionen:
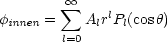
  $sum oo finnen = AlrlPl(cosh) l=0$
  Aufgrund der Axialsymmetrie gibt es keine -Abhängigkeit:
  $sum oo [ l -(l+1)] faußen = Blr + Clr Pl(cosh) l=0$
  Für r bleibt als führender Anteil nur das konstante elektrische Feld:
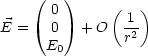
  $( ) 0 ( 1) E = 0 + O r2 E0$
  Somit gilt für das Potential:
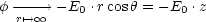
  $f -----> - E0 .r cos h = -E0 .z r'-->o o$
  Damit folgt für die Koeffizienten B_l:
  $B1 = -E0$
  
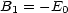
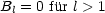
  $Bl = 0 f¨ur l > 1$
  Wir definieren B₀ = 0 als Nullpunkt des Potentials. Für die Randbedingungen gilt:
  - E ist stetig in tangentialer Richtung. $Eh(innen) = Eh(außen)$
    
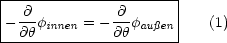
    $|---------------------| | @ @ | - @hfinnen = - @hfaußen (1) -----------------------$
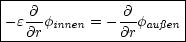
  - D ist stetig in radialer Richtung. $|----------------------| | @ @ | - e@rfinnen = -@r-fauß en | ------------------------$
    
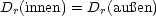
    $Dr(innen) = Dr(außen)$
    
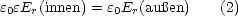
    $e0eEr(innen) = e0Er(außen) (2)$
  Wir betrachten nun:
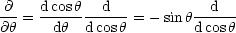
  $-@-= d-cosh--d---= - sinh --d--- @h dh dcosh dcosh$
  
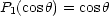
  $P1(cosh) = cosh$
  Somit gilt folgende Bilanzgleichung:
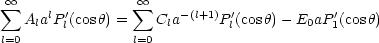
  $oo oo sum AlalP'(cos h) = sum Cla-(l+1)P'(cosh)- E0aP '(cosh) l=0 l l=0 l 1$
  Dies muß für jedes l getrennt gelten. l = 0 trägt nicht bei (P₀' = 0). Für l = 1 folgt:
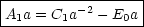
  $|-----------------| |A1a = C1a-2- E0a | ------------------$
  Wir erhalten als ersten Satz von Gleichungen:
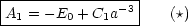
  $|---------------3-| -A1-=--E0-+-C1a---| (*)$
  
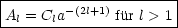
  $|---------------------| |Al = Cla-(2l+1) f¨ur l > 1 -----------------------$
  Für den radialen Sprung (Gleichung 2) gilt:
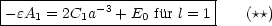
  $|------------3-------------| --eA1-=-2C1a--+-E0-f¨ur l =-1 (**)$
  
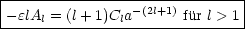
  $|-----------------------------| - elAl = (l+ 1)Cla- (2l+1) f¨ur l > 1 -------------------------------$
  Durch Kombination dieser beiden Gleichungen folgt dann schließlich:
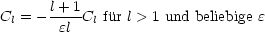
  $l+ 1 Cl = - -el-Cl f¨ur l > 1 und beliebige e$
  
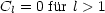
  $Cl = 0 f¨ur l > 1$
  
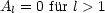
  $Al = 0 f¨ur l > 1$
  Wir addieren die Gleichungen (*) und (**):
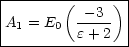
  $|---------------| | ( -3 ) | |A1 = E0 e+-2- | -----------------$
  
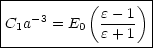
  $|----------(-----)-| C1a- 3 = E0 e--1- | ------------e-+1----$
  Für C₀ = 0 gibt es keinen 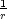-Term. Mit B₀ = C₀ = 0 wird das Potential normiert.
  $( ) -3--- ' finnen = - e+ 2 E0rP1(cos(h)) z$
  
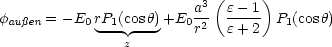
  $3( ) faußen = -E0 rP1(cosh)+E0 a- e--1- P1(cosh) --- --- r2 e+ 2 z$
  Innen hat man somit ein konstantes Feld in z-Richtung mit der Strärke E₀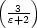. Außen existiert ein konstantes Feld in z-Richtung mit Stärke E₀ plus Dipolfeld mit dem Dipolmoment p:
  $( ) p = 4pe0 e--1- E0a3 e+ 2$
Magnetostatik: $|------------| \~/ × H = j(x)| -------------$
Da es keine Quellen des Magnetfelds gibt, gilt:
$|-------| - \~/ B-=-0|$
Wir definieren die Größe H durch eine Kombination mit dem -Feld in der Magnetisierung (molekulare Ströme):
$H = B - m0M$
Die Maxwell-Gleichungen in Materie lauten:
$@ \~/ × E +--B = o @t$

$\~/ .B = 0$

$\~/ .D = r$

$@- \~/ × H - @tD = j$

[prev] [prev-tail] [front] [up]