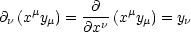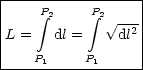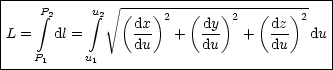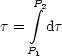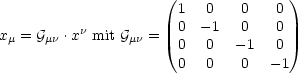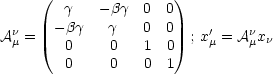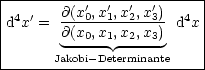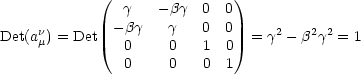5.1 Postulate der speziellen Relativitätstheorie
Gesucht ist die Transformation, die den Koordinatenachsen beschreibt und verträglich
mit den Postulaten der speziellen Relativitätstheorie ist.
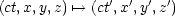
Spezielle Lorentztransformationen sind folgende:
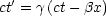
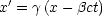
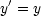
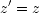
Wobei hier folgende Definitionen festgelegt werden:
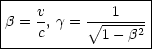
Im Grenzfall 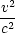 « 1 geht die Lorentz-Transformation in die Galilei-Transformation
über:
« 1 geht die Lorentz-Transformation in die Galilei-Transformation
über:
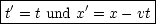
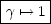
5.1.1 Fritz-Gerald-Lorentz-Kontraktion
Ein Stab der Länge L0 befinde
sich im System O' in Ruhe. x1', x2' seien Anfangs- und Endkoordinaten
des Stabes, wobei L0 = x2'- x1' gilt. Für die Koordinaten des Stabes gilt
nun:
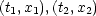
Die Lorentztransformation liefert folgenden Zusammenhang:

Wie mißt nun der Beobachter die Länge des Stabes in O? Dazu messen wir die
Länge des Stabes in O, indem wir gleichzeitig (t1 = t2) Anfangs- und Endpunkt
bestimmen. Die Länge L in O ist dann L = x2 - x1. Gleichung (*) liefert
nun:
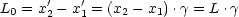
Damit folgt nun:
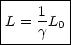
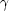 > 1 impliziert nun, daß L < L0. Diesen Effekt bezeichnet man als
Längenkontraktion
________________.
> 1 impliziert nun, daß L < L0. Diesen Effekt bezeichnet man als
Längenkontraktion
________________.
5.1.2 Zeitdilatation
Instabile Teilchen können als Uhren verwendet werden. Man
beobachtet verschiedene scheinbare Lebensdauern für verschieden schnelle Teilchen.
Wir stellen uns vor, daß sich ein Teilchen im System O' am Ursprung und in Ruhe
zur Zeit t1' = 0 erzeugt wird. Der Zerfall dieses Teilchen soll zur Zeit t2' = T0 (wahre
Lebensdauer im Ruhesystem des Teilchens) stattfinden. Wir haben somit zwei
Ereignisse, nämlich:
- Erzeugung: (0,0)
- Zerfall: (T0,0)
Was sind nun die Koordinaten der Ereignisse in O? Dazu verwenden wir nun genau
unsere Lorentztransformationen, womit folgt:
- Erzeugung: (0,0)
- Zerfall am Ort
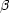 . c . T zur Zeit T, da sich O ja natürlich um v . T =
. c . T zur Zeit T, da sich O ja natürlich um v . T = 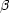 cT
weiterbewegt hat.
cT
weiterbewegt hat.
Wie groß ist nun die scheinbare Lebensdauer T? Nun gilt ja folgender Zusammenhang
mit der Lorentztransformation:
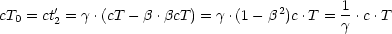
Dann ergibt sich mit 1 - 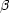 2 =
2 = 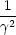 :
:
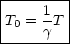
Die Lebensdauer der Myonen ist somit im bewegten System größer.
5.1.3 Eigenzeit
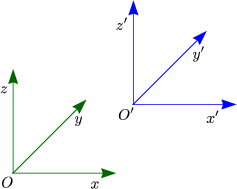
Folgende Analogie gibt es im dreidimensionalen Raum 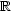 3. Wir
besprechen nun Drehungen statt Lorentz-Transformationen. Eine Größe, die invariant
unter Drehungen ist, ist der Betrag eine Vektors:
3. Wir
besprechen nun Drehungen statt Lorentz-Transformationen. Eine Größe, die invariant
unter Drehungen ist, ist der Betrag eine Vektors:
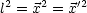
Infinitesimal bedeutet dies:
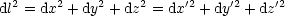
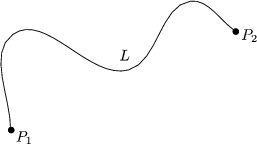
Die Länge eines Kurvenstücks berechnet sich folgendermaßen:
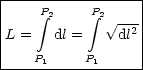
Eine Kurve kann in verschiedenen Koordinatensystemen auf unterschiedliche Art
und Weise parametrisiert werden:
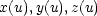
Es handelt sich als um drei Funktionen, wobei u1 < u < u2. Wir interpretieren nun
obige Formel für die Längenberechnung eines Kurvenstücks:
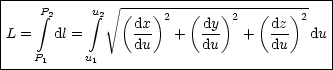
Gegeben sei nun eine Funktion F(l), die entlang der Bahnkurve definiert ist.
 liefert bei Berechnung in verschiedenen Koordinatensystemen und mit
verschiedenen Parametrisierungen immer das gleiche Resultat. Entsprechend für
Lorentz-Transformationen wissen wir, daß c2
liefert bei Berechnung in verschiedenen Koordinatensystemen und mit
verschiedenen Parametrisierungen immer das gleiche Resultat. Entsprechend für
Lorentz-Transformationen wissen wir, daß c2 2 = c2t2 -
2 = c2t2 - 2 invariant unter eben
diesen Transformationen ist.
2 invariant unter eben
diesen Transformationen ist.
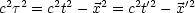
Dies sollte für spezielle Lorentztransformationen nachgerechnet werden. Infinitesimal
gilt hier wieder:
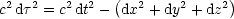
Beispiel:
Bei vorgegebener Geschwindigkeit 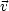 (t) gilt:
(t) gilt:
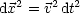
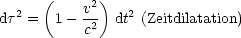
 ist hierbei die sogenannte Eigenzeit, die nun gegeben ist durch:
ist hierbei die sogenannte Eigenzeit, die nun gegeben ist durch:
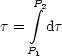
Dabei handelt es sich um die abgelaufene Zeit im Ruhesystem des Teilchens.
Beispiel:
Ein Elektron der Masse 0,51 MeV bewege sich auf einer Kreisbahn im
Beschleuniger (Umfang von 28 km) mit einer Energie von 51 GeV. Was ist nun die
abgelaufene Eigenzeit pro Umlauf?
5.1.4 Lorentz-Transformation, Vektoren, Tensoren
Wir erinnern uns hierbei an
Drehungen im euklidischen Raum:
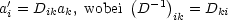
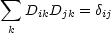
Die Summenkonvention schreibt vor, daß über den gemeinsamen Index k summiert
wird:
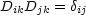
Die Spalten bzw. Zeilen sind orthonormiert, wobei c2t2 -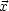 2 invariant ist. Hier
kommt der erste interessante Gesichtspunkt auf. c2t2 -
2 invariant ist. Hier
kommt der erste interessante Gesichtspunkt auf. c2t2 -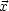 2 kann nämlich größer oder
kleiner als 0 sein! Wenn diese Kombination positiv ist, gibt es immer eine
Lorentztransformation, so daß die Raumkoordinaten verschwinden und nur die
Zeitkoordinaten übrig bleiben. Ist der Ausdruck kleiner als 0, so kann man die
Zeitkoordinaten verschwinden lassen, wobei nur die Raumkoordinaten erhalten
bleiben.
2 kann nämlich größer oder
kleiner als 0 sein! Wenn diese Kombination positiv ist, gibt es immer eine
Lorentztransformation, so daß die Raumkoordinaten verschwinden und nur die
Zeitkoordinaten übrig bleiben. Ist der Ausdruck kleiner als 0, so kann man die
Zeitkoordinaten verschwinden lassen, wobei nur die Raumkoordinaten erhalten
bleiben.
- Raumartig: c2t2 -
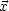 2 < 0
2 < 0
- Zeitartig: c2t2 -
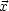 2 > 0
2 > 0
Wir verwenden Vierervektoren:
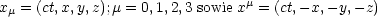
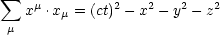
x nennt man kovariant und x
nennt man kovariant und x kontravariant. Wir können zwischen den beiden
Vektoren folgendermaßen transformieren:
kontravariant. Wir können zwischen den beiden
Vektoren folgendermaßen transformieren:
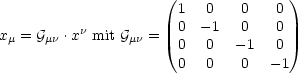
Es werden nur kovariante mit kontravarianten Indizes kontrahiert. Zwei
Indizes werden kontrahiert, heißt, daß ich über diesen gemeinsamen Index
summiere.
Die spezielle Lorentz-Transformation für die Bewegung in x-Richtung wird durch eine
Drehmatrix dargestellt:
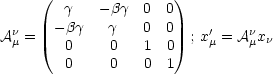
A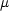
 ist eine Transformationsmatrix und kein Tensor! Damit haben wir die Analogie
zu Drehungen. Die allgemeine Lorentztransformation ergibt sich nun als Kombination
von Drehung und speziellen Lorentztransformationen. Unter Lorentztransformationen
gilt:
ist eine Transformationsmatrix und kein Tensor! Damit haben wir die Analogie
zu Drehungen. Die allgemeine Lorentztransformation ergibt sich nun als Kombination
von Drehung und speziellen Lorentztransformationen. Unter Lorentztransformationen
gilt:
- Lorentz-Skalare:
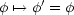
- Vektoren:
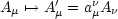
- Tensoren zweiter Stufe:

Ferner gilt:

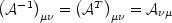
Zwei Lorentz-Transformationen in die gleiche Richtung mit 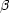 1 bzw.
1 bzw. 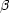 2 liefern eine
neue Lorentz-Transformation mit
2 liefern eine
neue Lorentz-Transformation mit 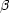 1+2 =?. Dieses Problem soll als Übung aufgefaßt
werden.
1+2 =?. Dieses Problem soll als Übung aufgefaßt
werden.
Beispiele für Vierervektoren:
Bestimme die Bahnkurve eines Teilchens (ct,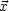 (t)).
Nichtrelativistisch gilt:
(t)).
Nichtrelativistisch gilt:
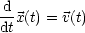
Hierbei handelt es sich um einer Dreier-Vektor. Relativistisch gilt jedoch:
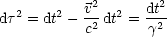
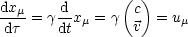
u ist die sogenannte Vierergeschwindigkeit. Das Quadrat von u
ist die sogenannte Vierergeschwindigkeit. Das Quadrat von u ist:
ist:
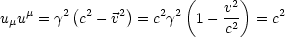
Evident im Ruhesystem des Teilchens ist folgendes:
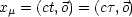
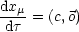
Nichtrelativistisch gilt:
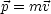
Für den relativistischen Impuls (Vierergruppe) folgt:
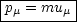
5.1.5 Volumenelement in 4 Dimensionen
In 3 Dimensionen gilt liefert 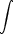 d3
d3 ein
invariantes Integral. Analog ist d4x ist invariant unter Lorentztransformationen, da
gilt:
ein
invariantes Integral. Analog ist d4x ist invariant unter Lorentztransformationen, da
gilt:
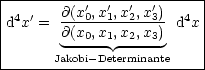
Das ist die Jakobi-Determinante, für die gilt:
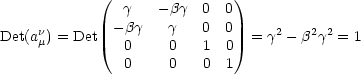
Für die Ableitungen gilt in 3 Dimensionen:
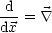
Hierbei handelt es sich um einen Vektor. In 4 Dimensionen gilt analog:
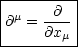
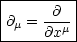
Anwendung:
In 3 Dimensionen gilt:

Für 4 Dimensionen folgt: