Die nichtrelativistische Lorentzkraft lautet:
Die Energieänderung eines geladenen Teilchens im Feld bei einer Verschiebung ist gegeben durch:
Wir betrachten nun die Energieänderung pro Zeiteinheit:
Die Gleichungen (*) und (**) sind vier Gleichungen für Komponenten. Der
F
-Tensor lautet:
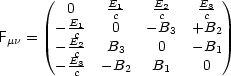
Damit können wir also mittels dieses Tensors schreiben:
Analog folgt für 
:
