6 Lorentzinvariante Formulierung der Elektrodynamik

[next] [prev] [prev-tail] [tail] [up]

Kapitel 6
Lorentzinvariante Formulierung der Elektrodynamik

6.1 Kovariante Formulierung der Lorentzkraft

Viererstrom:

Ausgangspunkt ist die Kontinuitätsgleichung:

|-----------| |@r | |@t-+ \~/ j = 0 -------------

Wir definieren = (c,) als Viererstrom.

@mj = @0j + @ij = --@--(cr)+ -@-j = 0 m 0 i @(ct) @xi i

^rj_r = 0 ist invariant, gilt also in jedem Bezugssystem. Wir definieren den Laplace-Operator:

[] = @20 - /_\

$/_\$ ist invariant unter Drehungen; ist invariant unter Lorentztransformationen. Die Wellengleichung für Potentiale (6.3) nach Anwendung der Lorentz-Eichung lautet:

|---------------------| |[]f = 1-r und []A = m0j| ------e0---------------

Wir verwenden ₀c₀ = und können damit schreiben:

[]f = c2m0r = m0c(cr)

Wir definieren nun A := als Vierervektor. Damit können wir die beiden obigen Wellengleichungen für die Potentiale und als eine einzige Gleichung notieren:

|-----------| |[]Am = m0jm | ------------

Die Lorentz-Eichung haben wir früher folgendermaßen definiert:

|-1-@-----------| |-2--f + \~/ A = 0| -c-@t-----------|

In unserer jetzigen Schreibweise lautet diese:

|-m-------| -@-Am-=-0-|

An dieser Stelle ist es außerdem sinnvoll, den Feldstärke-Tensor einzuführen:

Fmn = @mAn - @nAm

Dies ist ein antisymmetrischer Tensor. Er besitzt also 6 unabhängige Komponenten.

F00 = F11 = F22 = F33 = 0

1 @ 1 1 F0i = @0Ai - @iA0 = - c@tAi - \~/ cf = cEi

1 2 ( 1 2 ) ( ) F12 = @1A2 - @2A1 = - @ A2+@ A1 = - @ A2 - @ A1 = - \~/ × A 3 = - B3

Durch weitere Rechnung kann festgestellt werden:

F = B und F = -B 13 2 23 1

Damit können wir schließlich den Tensor notieren:

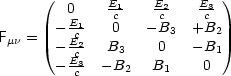
( ) 0 E1c Ec2 E3c - E1c 0 -B3 +B2 Fmn = - E2c B3 0 -B1 - E3c - B2 B1 0

Wir betrachten zunächst die inhomogenen Maxwell-Gleichungen:

@mFmn = @m(@mAn -@nAm) = []An - @n @mAm = m0jn -=0-

|-----------| @mFmn = m0jn| -------------

Für die homogenen Maxwell-Gleichungen folgt:

@-F---+-@-F--+-@-F---=-0| -c--mn---n-cm---m--nc-----

|-m ~-----| -@-Fmn-=-0-

Wir fassen zusammen:

Inhomogene Maxwell-Gleichungen: $\~/ .E =-1r e0$

$-@ \~/ × B - m0e0@t E = m0j$

$@mF mn = m0jn f¨ur n = 0,1,2,3 (*)$
Homogene Maxwell-Gleichungen: $\~/ .B = 0$

$\~/ × E + @B-= o @t$

$@mF~mn = 0 f¨ur n = 0,1,2,3 (**)$

~Fmn = 1emnrsFrs 2

ist ein total antisymmetrischer Tensor.

1 f¨ur m, n, r, s = 0, 1, 2, 3 und symmetrische Permutation { emnrs = -1 f¨ur antisymmetrische Permutation von {0,1,2,3} 0 sonst.

Analog zu ^ijk in 3 Dimensionen. (**) entspricht:

@cFmn + @nFcm + @mFnc = 0

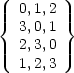Für , und = { 0,1,2}
3,0,1
2,3,0
1,2,3 .

[next] [prev] [prev-tail] [front] [up]