4.1 Einleitung

• Strom- und Stromdichte

  I sei der Strom, der durch einen Leitungsdraht.

  

  Die Einheit der Ladung ist das Ampere:

  

  Wir betrachten einen ausgedehnten Leiter:

  

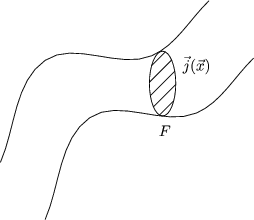
  () sei die Stromdichte am Punkt des Leiters. Durch Integration über die Querschnittsfläche folgt dann der Strom:

  

  Die Einheit von j ist:

  

  Durch das Prinzip der Ladungserhaltung folgt dann:

  

  Eine anschaulichere Interpretation erhalten wir in integraler Form:

  

  Wir vertauschen im linken Term zeitliche Ableitung und Integral, woraus folgt:

  

  Durch den Gaußschen Satz folgt nun:

  

  Q_V ist die Ladung im Volumen V . Die Abnahme der Ladung im Volumen V wird durch den Fluß des Stromes durch die Oberfläche von V kompensiert. Wir behandeln hier speziell die Magnetostatik, die zeitliche Änderung der Ladungsdichte muß also 0 sein:

  

  Daraus folgt, daß die Ströme divergenzfrei sind:

  

• Feldstärke B ( Dichte des magnetischen Flusses)

  Diese Größe wird zum Beispiel durch die Wirkung auf magnetischen Dipol (Kompaß-Ladung) gemessen. Wir wissen, daß es auf eine Kompaß-Ladung ein Drehmoment gibt: