4.2 Biot-Savartsches-Gesetz

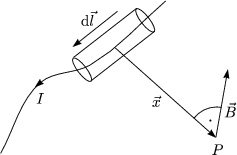
Das Gesetz beschreibt, wie man B aus dem Strom berechnen kann.

Das vom Strom I, vom Anteil dl des Drahtes am Punkt P erzeugte Feld ist gegeben durch folgende Beziehung (Biot, Savart):

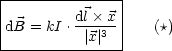
|---------------| |dB = kI .dl×-x-| (*) -----------|x|3--|

Wir haben hier ein -Verhalten (wie in der Elektrostatik), aber der Vektor-Charakter ist völlig anders. Die Konstante k lautet folgendermaßen:

m k = -0- 4p

In SI-Einheiten ist das 10^-7 . Im Gauß-System ist k = , wobei c die Lichtgeschwindigkeit ist. Im SI-System wird das auf die Definition von „Ampere“ führen.

Mikroskopische Interpretation:

I im Drahtstück d

ist der Strom, welcher durch die Bewegung der Ladung q mit der Geschwindigkeit

entsteht (v « c), also folgt:

I dl = qv

dB = m0qv-×-x 4p |x |3

Es gilt ja bekanntlicherweise:

q.x3-= 4pe0E am Punkt x |x|

Daraus folgt:

m0- v×-x- dB = 4p q|x|3 = m0e0v× E

Beispiel:

Wir betrachten einen unendlich langen geraden Draht im Abstand R vom Beobachter (P):

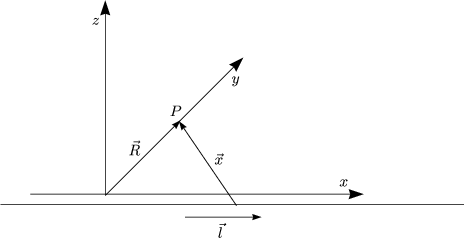
Wir drücken die Größen durch Vektoren aus:

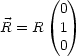
Lage des Beobachters: $( ) 0 R = R 1 0$
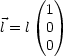
Richtung des Drahtes: $( ) 1 l = l 0 0$
Vektor vom Drahtstück d zum Beobachter: $x = l+ R$
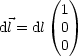
Drahtstück $( ) 1 dl = dl 0 0$

Für das Kreuzprodukt folgt:

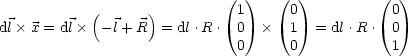
( ) (1 ) (0 ) (0) dl× x = dl× -l+ R = dl.R. 0 × 1 = dl.R . 0 0 0 1

Somit folgt durch Einsetzen in das Biot-Savart-Gesetz und anschließende Integration:

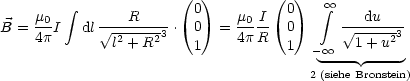
( ) ( ) m0 integral R 0 m0 I 0 integral oo du B = 4pI dl V~ -2---23-. 0 = 4p-R- 0 V~ ----23 l + R 1 1 - oo 1+ u 2 (siehe Bronstein)

Somit folgt als Endergebnis für :

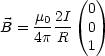
( ) m 2I 0 B = -0-- 0 4pR 1

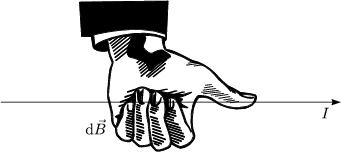
Es gilt die Rechte-Hand-Regel.

4.2.1 Kraft zwischen 2 stromdurchflossenen Leitern

Wirkung eines „äußeren“ magnetischen Feldes auf einen stromdurchflossenen Leiter
Wir stellen uns vor, daß der Strom I₁ im Leiterstück d ₁ fließt. Ein experimentelles Resultat ist:
$|--------------| dF1-=-I1dl1×-B-- (**)$
sei durch Strom I₂ im Leiter 2 induziert:
Wir nehmen an, daß Leiter 1 und 2 geschlossene Schleifen C₁ und C₂ bilden.
Die Kraft, welche von 2 auf 1 ausgeübt wird, folgt aus (*) und (**):
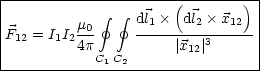
$|---------------------(-------)-| | m gf gf dl1 × dl2 × x12 | |F12 = I1I2-0- ---------3-----| | 4p C1C2 |x12| | ---------------------------------$

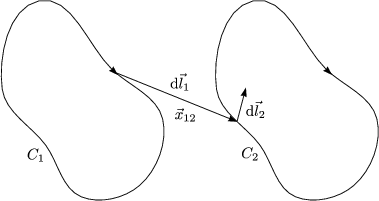
Es gibt die Grassmann-Identität, die ein doppeltes Kreuzprodukt auflöst:
$( ) a × b× c = b(a.c)- c(a.b)$
Somit folgt für den Zähler des Bruches:
$dl × (dl × x )= dl (dl .x )- (dl .dl ).x 1 2 12 2 1 12 1 2 12$
Wir verwenden folgende Beziehung:
$x12 1 |x12| 3 = - \~/ 1 |x12|$
Somit folgt:
$gf gf [ ( ) ( )] F12 = I1I2m0- - dl1dl2 -x12-- dl2 dl1 \~/ 1-1-- 4p |x12|3 |x13| C1C2$

$-1-- = ---1---- |x12| |x1 - x2|$
Es gilt durch Integration über einen Gradienten:
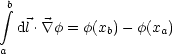
$integral b dl. \~/ f = f(xb) -f(xa) a$
Somit folgt durch eine geschlossene Integration:
$gf 1 dl1 . \~/ 1 |x-|= 0 C1 12$

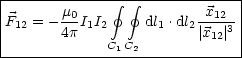
$|-------m----- gf - gf -------x---| |F12 = --0I1I2 dl1 .dl2-123| | 4p C1 C2 |x12| | -------------------------------$
Kraft zwischen zwei Drähten:
Aus Gleichung (**) und dem Resultat für B ergibt sich:
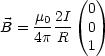
$( ) m02I 0 B = 4pR 0 1$
Dies gilt für einen unendlich langen Leiter. Außerdem folgt für die Kraft pro Längeneinheit eines Drahtes:
$|-------------| dF m02I1I2 | -dl = 4p--R-- | (***) ---------------$

$parallel } { attraktiv Strom antiparallel repulsiv$
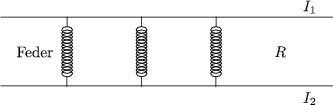
(* * *) gibt uns die Definition des Ampere.
$Kraft -7 Newton I1 = I2 = 1 Ampere ==> La¨nge-= 10 Meter--$
Einiges noch zur Definition des Ampere:
$N m0 =_ 4p10-7-2 A$
Wird ₀ experimentell gemessen, so findet man:
$|---------| |m0e0 =-1 | -------c2-|$

[next] [prev] [prev-tail] [front] [up]