4.3 Differentialgleichungen der Magnetostatik und Amperesches Gesetz

• Stromdichten:

• Gesetz von Biot-Savart:

Analog gilt in der Elektrostatik, wie wir gesehen haben:

Mit Gradientenschreibweise folgt:

Da der Gradient nur von abhängt, kann man ihn vor das Integral ziehen, woraus folgt:

An dieser Stelle wird es wieder nützlich, an die Analogie zur Elektrostatik zu erinnern. Offensichtlich gilt:

Dies ist ja einer der Fundamentalsätze der Vektoranalysis. Wenn ein Feld als Rotation eines anderen Feldes geschrieben werden kann, dann ist die Divergenz dieses Feldes 0. Das Ziel ist es nun, eine Differentialgleichung für von folgendem Typ zu finden:

Wir betrachten hiermit;

Das doppelte Kreuzprodukt lösen wir wieder mittels der folgenden Beziehung auf:

Somit folgt:

Nun gilt:

Wir setzen ein und ziehen den Gradienten in das Integral, woraus sich ergibt:

Der erste Term ist 0, was durch partielle Integration folgt, wobei die Randterme ignoriert werden.

Für den zweiten Term folgt dann durch Integration nach den Rechenregeln der Delta-Funktion:

Zur Herleitung der integralen Form, betrachten wir eine Fläche F mit dem Rand C:

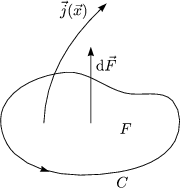
Das erste Integral schreiben wir mit dem Stokesschen Satz um, der besagt, daß man ein Flächenintegral über die Rotation ausdrücken kann durch ein Linienintegral über den Rand C der Fläche F. Das zweite Integral ergibt gerade den Strom I:

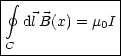
Wir haben das sogenannte Amperesche Gesetz hergeleitet. I ist dabei der Strom durch die Fläche.

Einfaches Beispiel:

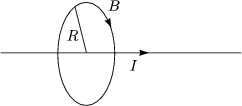
Wir betrachten einen geraden Leiter, dessen Feld kreisförmig um den Leiter herumläuft. Dann werden wir die obige Gleichung aus. Aus Symmetriegründen ist B tangential zum Kreis um den Leiter und vom Betrag her konstant wir R = const., woraus dann folgt, weil wir B vor das Integral ziehen können:

Somit folgt für das B-Feld:

Wir sehen, daß hier die Berechnung des Feldes mit dem Ampereschen Gesetz viel einfacher erfolgte, als mit dem Biot-Savart-Gesetz.

4.3.1 Vektor-Potential

Dies wäre ein mögliches Vektorpotential, wobei () eine beliebige Funktion ist, welche wegen ×(x) = 0 nichts zu B beiträgt. ist infolgedessen nicht eindeutig durch bestimmt. Falls ein Vektorpotential zu ist (d.h. × = ), so ist + ebenfalls ein Vektorpotential. Man spricht von der sogenannten Eichfreiheit. Dies haben wir auch schon beim Potential des elektrischen Feldes kennengelernt, wobei man eine beliebige Konstante zum Potential addieren konnte, ohne daß sich der Vektor des elektrischen Feldes änderte. Hier ist es aber viel raffinierter. Die Eichtransformation lautet:

In Gleichung (**) wählen wir = 0. Daraus folgt eine interessante Beziehung für :

Dies gilt wegen ^. = 0. Für das Vektorpotential gilt somit, daß nun die Divergenz 0 ist:

Man bezeichnet diesen Fall als Coulomb-Eichung. Aus × (×(x)) = ₀(x) folgt nun wieder durch Auflösung des doppelten Kreuzproduktes:

Es handelt sich hier um die Analogie zur Poisson-Gleichung in der Elektrostatik.

Anmerkung zu Eichtransformationen:

Also muß die Eichfunktion die Gleichung

= - erfüllen.