4.4 Lokalisierte Strme und magnetische Momente

4.4 Lokalisierte Ströme und magnetische Momente

sei ein im Volumen V von Null verschiedenes Feld, das wir im großen Abstand betrachten wollen. Wir gehen zur Komponentenschreibweise über:

i = 1,2,3 oder x,y,z

Wir betrachten das Vektorpotential im großen Abstand von einer lokalisierten Stromverteilung. Als Ausgangspunkt betrachten wir das Vektorpotential in Komponentenschreibweise:

integral ' Ai = m0- d3x'ji(x)'- 4p V |x - x|

Wir betrachten den Fall, daß ||»|'|: Damit können wir folgende Näherung benutzen:

--1---- 1-- x.x'- |x - x'| = |x| + |x| 3 +...

Wir erhalten nun für die Komponenten von :

integral integral A = -m0-- d3x'j (x)'+ --m0-- d3x'j(x')(x'.x) i 4p|x| i 4p|x|3 i ------I------ ----------II----------

Wir wollen nun zeigen, daß der Term I verschwindet, während sich der Term II folgendermaßen darstellen läßt:

Term II = m × x

Term I:
Mit $\~/$ _j'x_i' = _ij folgt:
$( ) \~/ ' x'i .j(x') = x'i \~/ 'j(x)+ji(x') (o) -- -- 0$
Mit dem Gaußschen Satz in abgewandelter Form folgt:
$integral integral integral d3x'ji(x') = d3x' \~/ '(x'ij(x')) = dF (x'i,j(x')) = 0 V V O$
Dieser Term ist 0, da j = 0 außerhalb von V . Der Monopolbeitrag verschwindet also, was uns ja nicht weiter wundert.
Term II:
Wir lassen die Konstante weg:
$integral integral integral 3 ' ' ' 3 '( ') ' 3 '[ ( ' ' )] d x(x .x)j(x) = d x xj(x ) x - d x x × x × j(x ) ------a------ ------ b------$
Wir zeigen, daß a = -b ist. Mit der Gleichung o zeigen wir:
$integral 3 ' ' ' integral 3 ' ' '( ' ') d x xjji(x) = d xx j \~/ xjj(x ) (***) V$
Durch partielle Integration folgt:
$integral ( ) integral d3x'x' \~/ ' x'j(x') = - d3x'x'jj(x')+ Randterme j j i ---0 --- V V$
Wir subtrahieren die Terme a und b, woraus sich dann ergibt:
$integral [ ( )] 2b = - dx' x× x'×j(x')$
Der Term II lautet somit:
$integral 1 3 '[( ' ') ] +2 d x x × j(x) ×x$

Damit folgt endgültig für das Vektorpotential:

|-----------------------------------------| | -m0--- 1 integral 3 '( ' ') | |A = 4p| x |3m × x mit m = 2 dx x ×j(x ) | -------------------------------------------

nennen wir das magnetische Dipolmoment und M(') = '×(') ist die sogenannte Dipoldichte. Wir wollen nun das resultierende Feld für berechnen:

( ) B = \~/ × A = m0 \~/ × m × -x3- 4p |x|

Wir lösen das doppelte Kreuzprodukt wiederum auf, woraus folgt:

m0 [ ( x ) ( ) x ] B = 4p- m \~/ .|x|3 - m . \~/ |x-|

Des weiteren gilt ja, daß der erste Term gleich 0 ist, da:

\~/ .-x-= - \~/ \~/ -1 = - /_\ -1-= 0 |x|3 |x |x|

Somit folgt:

|---------------------| | m03x-(m-.x)--mx2 | -B-=-4p------x5--------

Wir erkennen die Analogie zum elektrischen Dipol.

Einfache Beispiele:

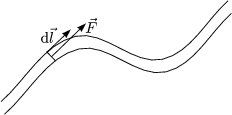
Stromschleife beliebiger Form in einer Ebene: $integral integral integral 3 d xj(x) = dldFj(x) = dlI$
() sei die Stromdichte und I der Strom.

$1 integral 1 gf m = - d3xx × j(x) = I- x × dl 2 V 2C$

_Schleife| × d | ist die Fläche, die von der Schleife umfahren wird.
Dies kann folgendermaßen begründet werden.
- Möglichkeit 1:
  Für infinitesimal kleine Winkel d gelte () ( + d). Dann kann auch d näherungsweise durch den Verbindungsvektor von () und (+d) ersetzt werden, wobei der Winkel etwa 90^o beträgt:
  $|x × dl| = |x|.|dl|.sin f ~~ |x|.|dl|$
  Wir haben hier also die Fläche des von den Vektoren und d aufgespannten Rechtecks. Damit wird die Fläche des Dreiecks bekommen, müssen wir einen Faktor berücksichtigen. Außerdem erhalten wir für dieses Dreieck:
  $|dl| sin(df) = |x| <==> |dl| = |x|sin(df) ~~ |x|df$
  Der letzte Schritt gilt für infinitesimal kleine d. Also folgt |×d | = ||² d. Wir erhalten damit folgende Beziehung:
  $1 gf 1 gf 2 2 | x × dl|= 2 |x| df Schleife Schleife$
  Dabei handelt es sich um die aus der Mathematik bekannte Sektorformel, welche die Fläche des Gebiets angiebt, welches von der Kurve C berandet wird.
- Möglichkeit 2:
  Wir legen folgendes fest:
  $( ) ( ) x = x , dl = dx y dy$
  Damit gilt also für das Kreuzprodukt:
  $( ) ( ) x dx x× dl = y × dy = ez .(x dy- ydx) 0 0$
  Damit gilt nun:
  $gf gf 1 |x × dl| = 1 (xdy - ydx) 2 2 Schleife Schleife$
  Mittels des Gaußschen Satzes in der Ebene erhalten wir außerdem folgende Erkenntnis:
  $integral integral 1 gf 1 d(x,y) = 2 (x dy- ydx) = 2I(G) G @G$
  Es handelt sich damit um den Inhalt der Fläche.
Also folgt für ||:
$|---------| ||m |= I .F| -----------$
steht senkrecht auf der Ebene.
Punktladungen q_i an den Punkten x_i mit Geschwindigkeiten v_i: $sum j(x) = qivid(x -xi) i$
x_i hängt hierbei von der Zeit ab:x_i(t). Damit folgt:
$1 integral 1 sum 1 sum ( p ) m = - d3xx × j(x) = - qi .(xi(t) ×v(t)) =- qi xi× --i 2 2 i 2 i Mi$
Mit dem Drehimpuls = × und der Masse M_i der Teilchen folgt:
$|-------------| | sum q L | |m = i--i | ------i--2Mi--$
Das System habe Teilchen, bei denen sich Ladung zu Masse gleich verhalten:
$-qi q-- Mi = M$
Somit ergibt sich:
$|----1-q- sum ------1-q--| |m = ---- Li = ---L | -----2M----------2M----$
ist hierbei der Gesamtdrehimpuls. Den Faktor
nennt man auch gyromagnetisches Verhältnis.

[next] [prev] [prev-tail] [front] [up]