Diese Kraft wollen wir jetzt in Verallgemeinerung von d![]() = I d
= I d![]() ×
×![]() für eine
Leiterschleife berechnen. Für das Drehmoment gilt:
für eine
Leiterschleife berechnen. Für das Drehmoment gilt:
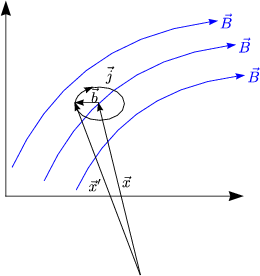
![]() (
(![]() ') sei am Punkt x' für langsam veränderlich:
') sei am Punkt x' für langsam veränderlich:
Dann gilt:
![]() =
= ![]() x
x![]()
![]() =
= ![]() ×
×![]() (
(![]() )
)
Folgende Näherung ist dabei sinnvoll:
Wir können ![]() somit als Konstante vor das Integral ziehen:
somit als Konstante vor das Integral ziehen:
Wir integrieren nur für kleine ![]() und machen eine Variablensubstitution
und machen eine Variablensubstitution ![]() '
'![]()
![]() und
setzen
und
setzen ![]() (
(![]() ')
')![]()
![]() (
(![]() ). Dann folgt:
). Dann folgt:
Das doppelte Kreuzprodukt wird wieder aufgelöst:
Gleichung (* * *) ist äquivalent zu: