4.6 Zeitabhängige Felder, Maxwell-Gleichungen

4.6.1 Faraday Gesetz

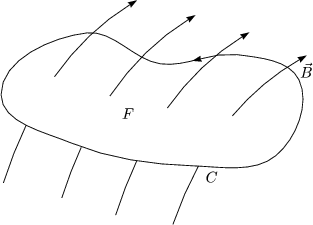
Der Fluß durch eine Leiterschleife C berechnet sich nach:

Die zeitliche Änderung von induziert eine Ringspannung oder elektromotorische Kraft. Diese Ringspannung E ist folgendermaßen definiert:

Dies ist das Faradaysche Gesetz. Das Vorzeichen ist bestimmt durch die Lenzsche Regel.

Extremes Beispiel:

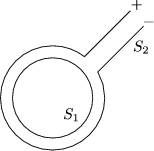
Zunächst sei der Strom in S₁ gleich Null und in S₂ ungleich Null. Ein Abschalten des Stromes in S₂ induziert einen Strom in S₁, so daß der Fluß ungeändert bleibt. Wir nehmen an, wir haben einen dünnen Leiter mit der Leitfähigkeit und dem Querschnitt f. Dann folgt:

Wir wollen nun einen Zusammenhang zwischen der Ringspannung und dem Strom herstellen:

sei parallel zu d . Außerdem folgt für die Stromdichte:

f ist der Querschnitt des Leiters. Dann ergibt sich:

l ist hierbei natürlich die Länge der Leiterschleife. Der Ausdruck ist einfach der Widerstand R des Leiters. E ist nun die Ringspannung, welche nötig ist, den Strom I gegen den Widerstand R aufrechtzuerhalten. Nach dem Faradayschen Gesetz ergibt sich nun für den induzierten Strom:

Mikroskopische Interpretation:

Diese Kraft wirkt auf einen bewegten Beobachter wie ein elektrisches Feld:

Die gestrichenen Größen sind diese im mitbewegten System. sei homogen. Wir stellen uns nun folgende Anordnung vor:

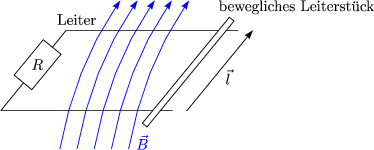
Des weiteren gilt folgende Beziehung zwischen der Fläche und der Geschwindigkeit, mit dem sich das Leiterstück bewegt:

Somit folgt mit B ^. Fläche = Fluß:

An dieser Stelle wollen wir zur differentiellen Form des Faradayschen Gesetzes übergehen. Wir wollen die Änderung des Flusses nur dadurch hervorrufen, daß wir das Magnetfeld ändern; die Fläche F sei zeitunabhängig.

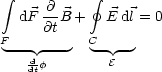
Das zweite Linienintegral wandeln wir mittels des Stokesschen Satzes in ein Flächenintegral um:

Nun folgt daraus:

Dies gilt für beliebige F. Wir nehmen an, daß das elektrische Feld auch unabhängig vom Leiter induziert wird. Daraus folgt eben, daß gelten muß:

Wir haben hier nun die differentielle Form des Faradayschen Gesetzes vor uns, dem in der Elektrotechnik eine sehr große Bedeutung zukommt.

4.6.2 Maxwell-Gleichungen

• Quellen des elektrischen Feldes:

• Magnetostatik:

• Faraday-Gesetz:

• Abwesenheit von magnetischen Monopolen:

Für zeitabhängige Ströme und Felder ist die Gleichung (*) inkonsistent. Wir bilden einfach die Divergenz:

Der erste Term ist immer 0, da die Divergenz einer Rotation immer 0 ist. Somit folgt:

Diese Inkonsistenz wurde nun von Maxwell beseitigt. Gleichung (*) wird nun in Analogie zum Faraday-Gesetz so abgeändert, daß durch + ₀ ersetzt wird. ist der sogenannte Verschiebungsstrom. Dann ergibt sich;

Dies folgt wegen der Kontinuitätsgleichung. Gleichung (*) wird somit ersetzt durch:

Wir fassen also zusammen:

• ^. =
• × - ₀₀ = ₀
• × - = 0
• ^. = 0

Die Gleichungen 1.) und 2.) nennt man inhomogene Maxwellgleichungen, 3.) und 4.) sind die homogenen Maxwellgleichungen. , , und hängen ab von und t. Empirisch folgt die sehr wichtige Gleichung

4.6.3 Übergang zu Vektor- und skalarem Potential

Also läßt sich diese Gleichung aufgrund der Wirbelfreiheit als Gradient eines skalaren Potential schreiben:

Also folgt:

Beide homogenen Maxwellgleichungen sind per Konstruktion erfüllt. Die Analogie in der Elektrostatik ist so, daß × = automatisch erfüllt ist, falls = -. Durch Bildung der Divergenz folgt für die erste inhomogene Maxwellgleichung:

Für die zweite inhomogene Maxwellgleichung gilt:

Wir haben hier ein gekoppeltes Differentialgleichungssystem vor uns. Die Entkopplung der Gleichungen erfolgt durch gezeigte Eichung. Wir wählen Potentiale speziell so, daß ^. + = 0. Aus der Lorentz-Gleichung werden 2 unabhängige Gleichungen:

Es besteht die Eichfreiheit, wodurch die Potentiale frei gewählt werden können. Wir wählen spezielle Potentiale:

Genauere Diskussion der Eichfreiheit:

Wegen = - - muß auch transformiert werden nach '-(,t). Man kann durch Eichtransformation immer erreichen, daß die Lorentzeichung erfüllt ist:

Falls und zwar das Magnetfeld und das elektrische Feld wie gewünscht liefern, aber ^. + 0 = f(,t), dann suchen wir (,t), so daß für neue Potentiale ' und ' folgendes gilt:

Die Forderung an sei nun folgendes:

ist Lösung der inhomogenen Wellengleichung. Eine Alternative wäre die sogenannte „Coulomb-Eichung“ oder „transversale Eichung“:

Dann folgt:

Die Poisson-Gleichung bleibt somit gültig, aber es ist ein Preis dafür zu bezahlen, weil dann nämlich die 2.Gleichung komplizierter wird:

Speziell für verschwindende Quellen = 0 und = folgt:

Die Wellengleichung für lautet:

Und natürlich gilt in diesem speziellen Fall: