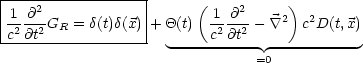4.7 Elektromagnetische Wellen im Vakuum
4.7.1 Mathematischer Einschub:Fourier-Zerlegung, Fourier-Integral
Ein Wellenzug
beliebiger Form soll als Überlagerung von e-i t+kx dargestellt werden. Wir erinnern
uns an dieser Stelle an Kapitel 3:Fourier-Reihen. Jede Funktion f(x) im Intervall
t+kx dargestellt werden. Wir erinnern
uns an dieser Stelle an Kapitel 3:Fourier-Reihen. Jede Funktion f(x) im Intervall
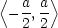 läßt sich darstellen als Fourier-Reihe:
läßt sich darstellen als Fourier-Reihe:
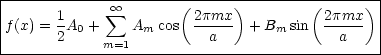
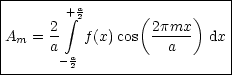
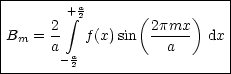
Das System ![{ V~ --[ ( ) ( )]}
2- sin 2pmx- ,cos 2pmx-
a a a](th966x.gif) ist orthonormiert und
vollständig
_________.
ist orthonormiert und
vollständig
_________.
Komplexe Darstellung:
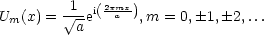
Eine beliebige komplexe Funktion in  kann nun dargestellt werden
als:
kann nun dargestellt werden
als:

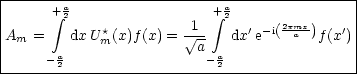
Für die Um gilt:
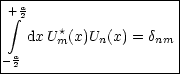
Das System ist also orthonormiert. Wir Vollständigkeit sei folgendermaßen
dargestellt:
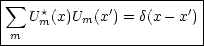
Die Wellenzahlen  nehmen nur diskrete Werte an. Mit wachsendem a liegen
diese Werte immer dichter. Das Verhalten für a
nehmen nur diskrete Werte an. Mit wachsendem a liegen
diese Werte immer dichter. Das Verhalten für a
 ist:
ist:
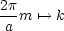
k nehme kontinuierliche Werte an.
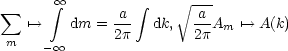
Und somit gilt:
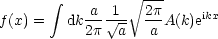
Erfreulicherweise kürzt sich a raus. Dann folgt:
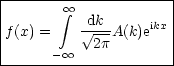
Mittels folgender Umkehrung kann A(k) berechnet werden:
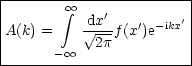
Vollständigkeit:
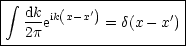
Wir vertauschen x und k:

Dies entspricht der Orthonormiertheit. Wir behaupten nun:
|
| |
| Die Lösung der Wellengleichung kann als Überlagerung von ebenen Wellen dargestellt werden. |
| |
|
| |

u(t, ) sei eine Lösung der Wellengleichung.
) sei eine Lösung der Wellengleichung.
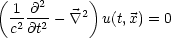
u(t,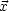 ) bei fester Zeit kann als Fouriertransformierte geschrieben werden:
) bei fester Zeit kann als Fouriertransformierte geschrieben werden:
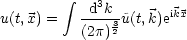
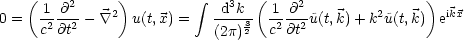
Damit folgt nun:
![integral 3 ikx [1 @2 2 ]
d ke c2@t2~u(t,k) +k u~(t,k) = 0](th989x.gif)
Somit muß der Ausdruck in der Klammer 0 ergeben:
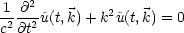
Dann erhalten wir folgende gewöhnliche Differentialgleichung:
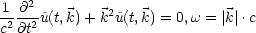
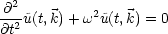
Die Lösungen dieser Differentialgleichung sind einfach trigonometrische Funktionen,
die man auch als komplexe Exponentialfunktion schreiben kann:
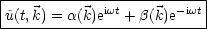
Eine allgemeine Lösung des Problems ist somit:
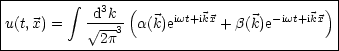
Die Funktionen  (
(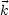 ) und
) und 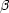 (
(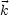 ) sind hierbei beliebig.
) sind hierbei beliebig.
Anfangswertproblem:
Es sei u(0,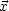 ) = a(
) = a( ) und
) und 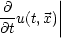 t=0 = b(
t=0 = b(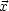 ) gegeben.
ã(
) gegeben.
ã(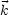 ) und
) und 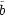 (
(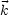 ) sind die Fouriertransformierten von a und b.
) sind die Fouriertransformierten von a und b.
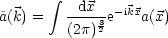
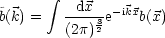
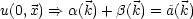
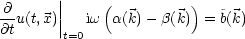
Somit folgt durch Auslösen:
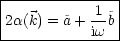
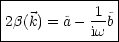
Spezielle Anfangsbedingung:
D(t,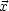 ) sei so gewählt, daß folgendes gelte:
) sei so gewählt, daß folgendes gelte:
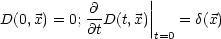
Dann folgt daraus:
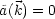
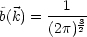
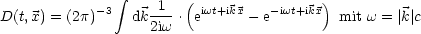
Wir wollen D nun auch noch explizit angeben:
![|---------------[-(------)----(------)]-|
| -1---1- |x-| |x|- |
|D(t,x) = 4pc2|x| d t- c - d t+ c |
-----------------------------------------](th1015x.gif)
Dies sollte nachgerechnet werden! D ist nur auf dem Lichtkegel ungleich
0.
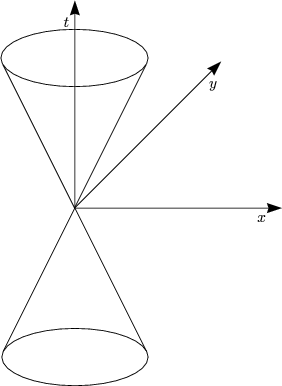
Die Wellengleichung ist:

Später werden wir die „retardierte“ Greensche Funktion benötigen:
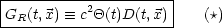
GR erfüllt die inhomogene Gleichung.
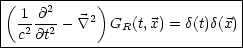
Dann gilt:
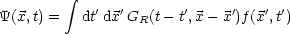
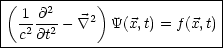
Wir wollen nun die Gleichung (*) beweisen. Dazu betrachten wir zunächst 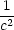
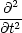 GR.
GR.
![1-@--@ 2 @--@ @-[ @- ] -@ [ @- ]
c2@t@tc Q(t)D(t,x) = @t@tQ(t)D(t,x) = @t d(t)D(t,x)+ Q(t)@tD(t,x) = @t D(0,x)+ Q(t)@tD(t,x) =
@ [ ]
= -- Q(t)D˙(t,x) = d(t)D ˙(t,x) + Q(t)D¨(t,x) = D˙(0, x)+ Q(t)D¨(t,x) = d(x) + Q(t)D¨(t,x)
@t](th1024x.gif) | (4.1) |
Somit ergibt sich nun:
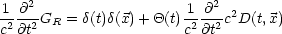
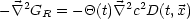
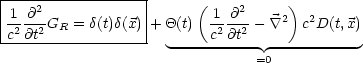
Im folgenden wollen wir nun die Polarisation einer elektromagnetischen Welle
besprechen. Damit wiederholen wir:
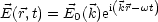

Wobei  = |
= |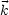 |. c ist.
|. c ist.
- Die beiden Ansätze erfüllen die Wellengleichung.
- Nur der Realteil ist physikalisch sinnvoll.
- Außerdem muß
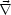
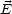 = 0 und
= 0 und 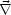
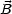 = 0 gelten.
= 0 gelten.
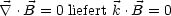
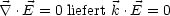
Ferner folgt aus 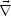 ×
×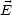 = -
= -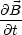 .
.

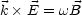
Analog folgt:
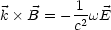
Die Vektoren 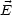 0,
0, 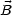 0,
0, 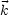 stehen paarweise senkrecht aufeinander. Man sollte
nachrechnen, daß
stehen paarweise senkrecht aufeinander. Man sollte
nachrechnen, daß  oder
oder  senkrecht zur Ausbreitungsrichtung stehen. Es handelt
sich also um transversale Wellen.
senkrecht zur Ausbreitungsrichtung stehen. Es handelt
sich also um transversale Wellen.
4.7.2 Polarisation
Wähle spezielles Koordinatensystem:
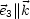
Falls 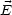 ~
~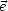 1 oder
1 oder  ~
~ 2, ist
2, ist 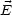 linear polarisiert. Allgemein hat man:
linear polarisiert. Allgemein hat man:
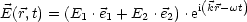
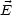 1 und
1 und 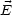 2 sind dabei komplex.
2 sind dabei komplex.
Spezialfälle:
![]() = 0 und
= 0 und ![]() =
= ![]() . Ausgangspunkt ist wieder
das System der Maxwell-Gleichungen:
. Ausgangspunkt ist wieder
das System der Maxwell-Gleichungen:
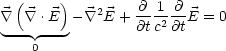
![]() erhalten. Analog folgt für
erhalten. Analog folgt für ![]() :
:
![]() und
und ![]() erfüllt die Wellengleichung:
erfüllt die Wellengleichung:
![]() habe hier eine beliebige Richtung und es gelte
habe hier eine beliebige Richtung und es gelte ![]() 2 = 1. Wir wollen
beweisen, daß f(
2 = 1. Wir wollen
beweisen, daß f(![]() ,t) die Wellengleichung erfüllt. Es gilt durch Anwendung
des Laplace-Operators:
,t) die Wellengleichung erfüllt. Es gilt durch Anwendung
des Laplace-Operators:
![]() mit der Geschwindigkeit c. In einer
Dimension ergibt sich:
mit der Geschwindigkeit c. In einer
Dimension ergibt sich:
![]() sei die Ausbreitungsrichtung und
sei die Ausbreitungsrichtung und ![]() die
Frequenz. Die Ausbreitungsgeschwindigkeit c ist unabhängig von
die
Frequenz. Die Ausbreitungsgeschwindigkeit c ist unabhängig von ![]() bzw.
bzw.
![]() . Eine allgemeine Lösung der Wellengleichung kann als Überlagerung von
ebenen Wellen dargestellt werden. Dazu müssen wir uns kurz mit dem
Problem der Fourier-Zerlegung beschäftigen.
. Eine allgemeine Lösung der Wellengleichung kann als Überlagerung von
ebenen Wellen dargestellt werden. Dazu müssen wir uns kurz mit dem
Problem der Fourier-Zerlegung beschäftigen.
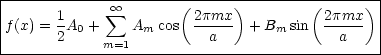
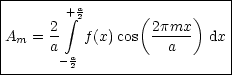
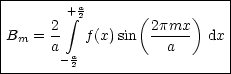


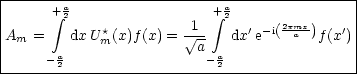
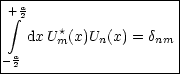
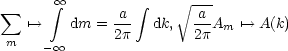
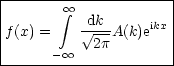
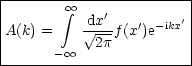

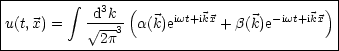

![1-@--@ 2 @--@ @-[ @- ] -@ [ @- ]
c2@t@tc Q(t)D(t,x) = @t@tQ(t)D(t,x) = @t d(t)D(t,x)+ Q(t)@tD(t,x) = @t D(0,x)+ Q(t)@tD(t,x) =
@ [ ]
= -- Q(t)D˙(t,x) = d(t)D ˙(t,x) + Q(t)D¨(t,x) = D˙(0, x)+ Q(t)D¨(t,x) = d(x) + Q(t)D¨(t,x)
@t](th1024x.gif)