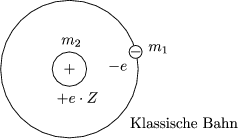

Wir zerlegen das Problem in Schwerpunkt- und Relativ-Koordinaten. Hierbei gilt nun außerdem (siehe Theoretische Physik B):
Für eine kanonische Transformation gilt [pj,xk] = ![]() jk. Für die reduzierte Masse
jk. Für die reduzierte Masse ![]() und die Gesamtmasse M gilt:
und die Gesamtmasse M gilt:
Damit können wir für die Hamilton-Funktion schreiben:
Wir gehen nun zur Quantenmechanik über, verwenden also Operatoren:
Damit gilt dann für stationäre Zustände:
Für den Hamilton-Operator folgt damit:
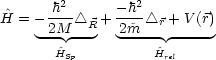
Die Wellenfunktion ![]() (
(![]() ,
,![]() ) kann als Produkt formuliert werden, da
H = HSp(
) kann als Produkt formuliert werden, da
H = HSp(![]() ) + Hrel(
) + Hrel(![]() ):
):
Für ![]() Sp(
Sp(![]() ) verwenden wir den Ansatz exp
) verwenden wir den Ansatz exp![]() . Damit gilt also:
. Damit gilt also:
Wir haben ein maximales System vertauschbarer Operatoren. Aus den 6 Freiheitsgraden ergeben sich 11 Bewegungsintegrale bzw 6 involutorische Bewegungsintegrale mit {H,Ik} = 0 und {[I,Ik} = 0.
![]() rel (n),
rel (n), ![]() 2
(l),
2
(l), ![]() z (m)
z (m)
Wir suchen das gemeinsame System der Eigenfunktionen zu ![]() rel,
rel, ![]() rel2,
rel2, ![]() z,rel.
z,rel.
Durch R(r) erhalten wir die beiden Quantenzahlen n und l.
a sei der Bohrsche Radius. Für das Potential des Wasserstoffatoms gilt:
![[( ) ] [ ]
^ h2- 1--@- 2@R- --h2- 2
HY(r) = - 2m r2@r - r @r .Ylm(h,f) + 2m~r2 L YlmR +V (r)RYlm = ERYlm
---------Kinetische Energie-------- Rotationsenergie-
der Radialbewegung](th602x.gif)
Für die radiale Bewegung gilt:
Somit gilt für den Operator des Radialimpulses:
Ist ![]() r = -i
r = -i![]()
![]() ? Nein! Es gilt aber:
? Nein! Es gilt aber:
Es folgt die Radialgleichung mit ![]() 2Y lm =
2Y lm = ![]() 2l(l + 1)Y lm:
2l(l + 1)Y lm:
Wir untersuchen das asymptotische Verhalten von R(r) für r![]()
![]() :
:
Die Funktion ist nicht normierbar; es handelt sich um keinen gebundenen Zustand.
Hierbei haben wir einen gebundenen Zustand.
Zukünftig wird nur der Fall E < 0 betrachtet. Wir führen die Längeneinheit ![]() ein:
ein:
Außerdem werden folgende dimensionslose Variablen verwendet:
![2 l(l+ 1) [2 ~m 1 Ze2] 1 [2~m ]
R~''(r)+ r ~R(r)+--r2--~R(r)+ h2-.c2 .4pe .-c-- .r.R~(r) = h2-c2Ryj R~(r) = 0
-------- -0------ ---- ----
V~ 2j !=1](th621x.gif)
Nun steckt der Energieeigenwert in ![]() . Wir machen folgenden Struktur-Ansatz:
. Wir machen folgenden Struktur-Ansatz:
Außerdem stellen wir folgende Forderung:
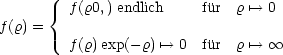
Ist P(![]() ) ein Polynom? Durch Einsetzen erhalten wir eine Differentialgleichung für
f(
) ein Polynom? Durch Einsetzen erhalten wir eine Differentialgleichung für
f(![]() ):
):
Wir machen nun einen erneuten Ansatz für f(![]() ) in Form eines verallgemeinerten
Potenzreihenansatzes:
) in Form eines verallgemeinerten
Potenzreihenansatzes:
![]() könnte sogar nicht ganzzahlig sein, aber es muß
könnte sogar nicht ganzzahlig sein, aber es muß ![]() > 0 gelten.
> 0 gelten.
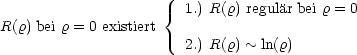
Mittels eines Koeffizientenvergleichs ergibt sich dann:
Daraus ergibt sich dann ![]() = l (
= l (![]() = -(l + 1)).
= -(l + 1)).
![[ ]
Ck+1 [(k+ 1 + b)(k+ 2+ b) - l(l+ 1)] = 2Ck (k+ 1 + b)- V~ 1
------- ------n
!=0](th630x.gif)
Es handelt sich um eine zweigliedrige Rekursionsformel. Wir untersuchen das
Verhalten der P(![]() )-Reihe für
)-Reihe für ![]()
![]()
![]() , also k
, also k![]()
![]() :
:
Daraus ergibt sich dann:
Für beliebige ![]() bricht die Reihe nicht ab.
bricht die Reihe nicht ab.
Die Funktion ist nicht normierbar, aber wir können selbst dafür sorgen, daß die Reihe abbricht. Dazu setzen wir:
Die Reihe bricht nun ab mit k - n - (1 + l) > 0, d.h. l < n - 1.
P(![]() ) sind mit den Laguerreschen Polynomen verwandt.
) sind mit den Laguerreschen Polynomen verwandt.
Die Laguerre-Polynome Ln(x) sind folgendermaßen zu bilden:
Die zugeordneten Legendre-Polynome sind definiert durch (siehe harmonischer Oszillator):
Wir erhalten also folgendes Resultat für die Wellenfunktion:
| n | l | Rnl |
| 1 | 0 | exp |
| 2 | 0 | |
| 2 | 1 | r . exp |
Hierbei handelt es sich um ein e+-e--System
Dies ist ein gebundenes Elektron-Loch-Paar im Halbleiter.
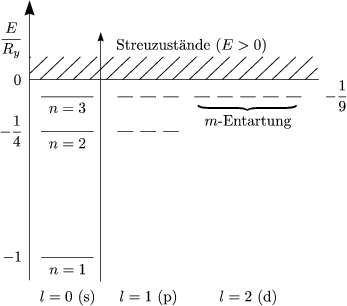
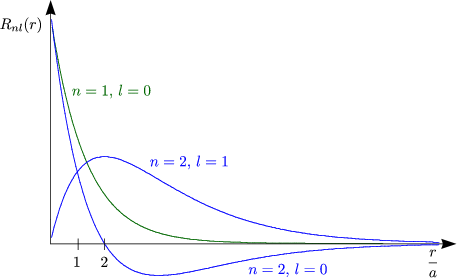
Die radiale Ortswahrscheinlichkeit berechnet sich durch:
Das r2 ergibt sich durch Verwendung von Kugelkoordinaten. Das Maximum befindet sich bei r = n2a. Klassisch handelt es sich für l < n - 1 um Ellipsenbahnen.
Die Wellenfunktionen sind orthogonal:
n = 1 und n = 2, l = 1 sind bei Radialfunktion positiv.
Enlm ist für alle Zentralpotentiale von m unabhängig. Dies kommt aufgrund der Kugelsymmetrie, da keine Richtung für die z-Achse ausgezeichnet ist.
Dabei handelt es sich um die Besonderheit des ![]() -Potentials. Im
allgemeinen gilt:
-Potentials. Im
allgemeinen gilt:
Betrachten wir die Bahn klassisch:
![]() vertauscht nicht mit
vertauscht nicht mit ![]() 2. Aber es gibt doch immer ein fünftes
Bewegungsintegral für jedes Zentralproblem.
2. Aber es gibt doch immer ein fünftes
Bewegungsintegral für jedes Zentralproblem.
Der Ausweg ist:
Wir machen dies zu einem Operator, also:
Der reziproke Operator ist wie folgt definiert:
Wenn der Eigenwert gleich Null ist, dann existiert kein reziproker Operator.
Für ein freies Teilchen gilt:
Dies gilt für -![]() < k <
< k < ![]() .
.
Für das Dipolmoment gilt:
Wobei gilt:
Hierbei handelt es sich um die sogenannten Matrixelemente des Dipolmoments. Dieses oszilliert mit:
Für die Energie des Atoms gilt:
Für die Eigenzustände ![]() i und
i und ![]() f gilt:
f gilt:
Also gilt:
Dies ist einsichtig aufgrund der Erhaltung der Energie. Aus Theorie C übernommen:
Wir machen folgenden Ansatz:
Es gilt hiermit:
Die Energieänderung beträgt:
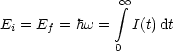
Hieraus kann nun ![]() bestimmt werden. Für die Zerfalls-Rate gilt:
bestimmt werden. Für die Zerfalls-Rate gilt:
Wir führen Kugelkoordinaten ein:
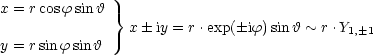
Für den Übergang l = 1![]() l = 0 gilt:
l = 0 gilt:
Wir haben in Ausbreitungsrichtung zirkular polarisiertes (mathematisch positiver Drehsinn) Licht.
Die Auswahlregeln für einen beliebigen Zustand sind ![]() l = ±1,
l = ±1, ![]() m = 0, ±1. Für
Quadrupol-Übergänge gilt außerdem
m = 0, ±1. Für
Quadrupol-Übergänge gilt außerdem ![]() l = 2:
l = 2: