[next] [prev] [prev-tail] [tail] [up]

3.10 Ausstrahlung elektromagnetischer Wellen durch angeregten Zustand

PIC

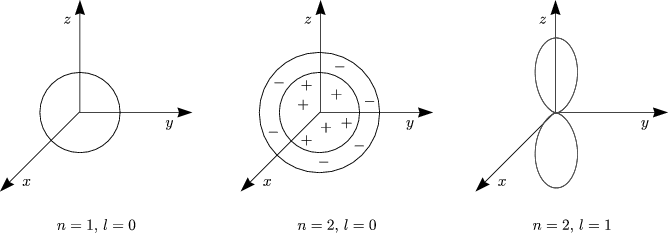
Atom <==> Maxwell-Feld Wir führen eine halb-klassische/-quantenmechanische Beschreibung ein. Das Atom wird hierbei quantenmechanisch und das elektromagnetische Feld klassisch beschrieben.

{ Absorption Elektromagnetisches Feld Induzierte Emission Spontane Emission

Das Atom wird durch die Wellenfunktion Y(r,t) beschrieben:

( ) ( ) Y(r,t) = CiYi(r).exp -iEi-.t + CfYf (r.exp -iEf-.t h h

Hierbei sei der Anfangszustand mit i („initial“) und der Endzustand mit f („final“) bezeichnet. Wir berechnen den Erwartungswert des elektrischen Dipolmoments:

integral ^ d(t) = Y*(r,t)dY(r,t)d3r

Für den Dipoloperator p^ gilt:

^p = er2- er1 = - er

Damit resultiert:

integral d(t) = - e |Y(r,t)|2 .rd3r

Damit folgt nun mit Ci = |Ci|. exp(ifi) und Cf = |Cf|. exp(iff):

[ ( E - E )] |Y |2 = |Ci|2 .|Yi(r)| 2 + |Cf|2 .|Yf (r)| 2 + CiCf YiY*f exp - i-i--ft = [ h( )] = |Ci|2 .|Y1(r)|2 + |Cf |2 .|Yf (r)| 2 + C|iCf |Yi(r)Y* (r)exp - iEi---Eft +if f h
(3.8)
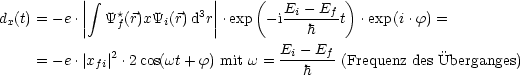|i ntegral | ( ) d (t) = - e.|| Y*(r)xY (r)d3r||.exp - iEi---Eft .exp(i.f) = x | f i | h 2 Ei- Ef = - e.|xfi| .2cos(wt + f) mit w =---h---(Frequenz des ¨Uberganges)
(3.9)
Das zeitabhängige Dipolmoment strahlt mit der Intensität I:
------- (¨ )2 I ~ d(t)

„ “ bedeutet hierbei der zeitliche Mittelwert.

I = -1--4e2w4|C (t)C (t)| 2(|x | 2 + |y |2 + |z |2) (durch Wechselwirkung mit elektromagnetischem Feld) 4pe0 3c3 i f fi fi fi

[next] [prev] [prev-tail] [front] [up]