![]() ist der kanonische Impuls -i
ist der kanonische Impuls -i![]()
![]() . Der kinetische Impuls folgt durch:
. Der kinetische Impuls folgt durch:
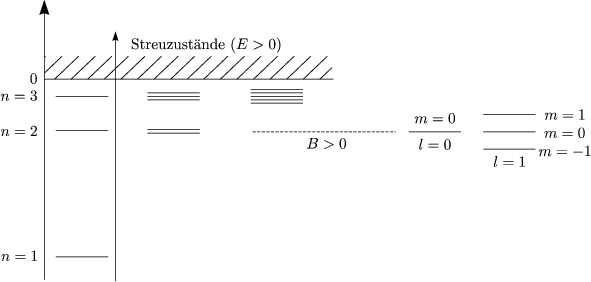
Für die Entartung ergibt sich dann:
Wir berechnen das magnetische Moment durch:
Das ![]() -Feld wird durch ein Vektorpotential charakterisiert:
-Feld wird durch ein Vektorpotential charakterisiert:
Beispielsweise gilt für ![]() = (0,0,B):
= (0,0,B):
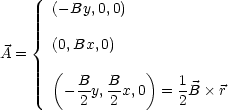
Der Operator ist - Gott sei Dank - vertauschbar, falls div ![]() = 0 ist, was hier auch
gilt (
= 0 ist, was hier auch
gilt (![]() xÂx = Âx
xÂx = Âx![]() x, da
x, da ![]() x mit y vertauscht).
x mit y vertauscht).
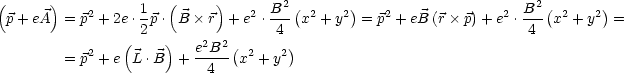 | (3.7) |
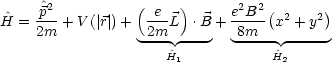
Wir vernachlässigen nun den Operator ![]() 2 für kleine
2 für kleine ![]() -Felder, woraus sich dann
ergibt:
-Felder, woraus sich dann
ergibt:
![]() ,
, ![]() 2
und
2
und ![]() z ist dabei ein maximales System vertauschbarer Bewegungsintegrale.
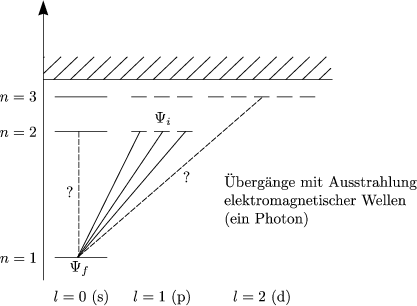
Die Eigenzustände ergeben sich durch Betrachtung der Schrödinger-Gleichung:
z ist dabei ein maximales System vertauschbarer Bewegungsintegrale.
Die Eigenzustände ergeben sich durch Betrachtung der Schrödinger-Gleichung:
![]() und
und ![]() 0 haben dieselben Eigenzustände:
0 haben dieselben Eigenzustände:
Wir definieren geschickterweise das sogenannte Bohrsche Magneton: