3.8 Drehimpulseigenzustände

Wir betrachten den Drehimpuls-Operator = ( _x, _y, _z) mit [ _x, _y] = i _z (und zyklisch). Da [ ² , _z] = 0 ist, existiert ein gemeinsames System von Eigenfunktionen |,m> mit:

Beweis in fünf Schritten:

• Leiteroperator:
  

• Es gilt > m²!

  Die Voraussetzung dazu ist:

  

  Daraus ergibt sich dann:

  

  Das heißt also:

  

• _±|m> ist Eigenzustand zu _z (mit dem Eigenwert m = ±1) un zu ² mit dem Eigenwert .
  

  Es folgt somit:

  

  Da [ ² , _±] = 0 gilt, können wir ² und _± vertauschen:

  

• Nach Punkt 2 ist m² < ; es muß also (zu festem , das wir aber noch nicht kennen) einen größten m-Wert geben, für den die „m-Leiter“ nach oben abbricht. Für m_max := j ist ₊|,j> = 0, womit sich ergibt:

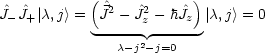
  Analog existiert ein kleinster m-Wert j'; die Leiter bricht nach unten ab für _-|,j> = 0, womit -j'² -j' = 0 folgt. Beide Forderungen sind nur möglich, wenn = j(j + 1) = j'(j'- 1) ist, das heißt j' = -j. (j' = j + 1 scheidet aus, da m_min > m_max wäre.

• Welche j-Werte sind möglich?

  Ausgehend vom kleinsten m-Wert (= -j) erreichen wir durch N-fache Anwendung von ₊ den größtem m-Wert (= j).

  

  Es muß also -j +N = j gelten; es ist nun N = 2j, woraus sich die Werte j = 0, , 1, , 2, ... ergeben.

Unterscheide nun folgende Fälle:

• j = 0, 1, 2, ... (m = -j, -j + 1, ..., j)

  Hierbei handelt es sich um 2j + 1 Werte. Darunter fällt auch der Bahndrehimpuls = × eines Teilchens, aber auch die Eigendrehimpulse (=Spin) von Bosonen (und deren Gesamtdrehimpulse = + ).

• j = , , , ... (j_z = -j, -j + 1, ..., j)

  Auch hier liegen 2j + 1 Werte vor. Es gibt jedoch dazu kein klassisches Analogon. Hierunter fallen die Eigendrehimpulse von Fermionen (und deren Gesamtdrehimpulse = + ).

Zusammenfassung: (Änderung der Notation bezüglich und m)

Für festes j läßt sich |j,j_z> als (2j + 1) × (2j + 1)-Matrix darstellen, beispielsweise für l = j = 1 als 3 × 3-Matrix:

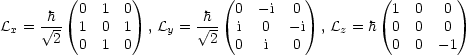
Allgemein gilt:

Beispiele:

• Starre Hantel oder Keil

  

• Isotroper Rotator

  

Für den Drehimpulsoperator gilt:

Der Operator ist hermitesch:

Für die Kommutatoren gilt:

Man nennt folgende Größen vertauschbare Integrale der Bewegung:

Es handelt sich um simultane Eigenzustände. Wir haben folgende Eigenwertprobleme:

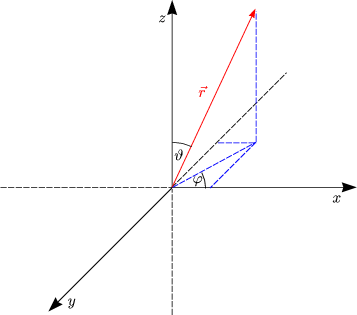
Bei m handelt es sich um 2l + 1 Werte. Die Eigenfunktionen des Problems sind die sogenannten Kugelflächenfunktionen _l,m(,) = Y _l,m(,). Aus Symmetriegründen betrachten wir das ganze in Kugelkoordinaten (x, y, z r, , ):

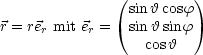
Für den Gradienten in Kugelkoordinaten gilt:

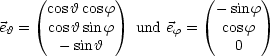
Weiterhin gilt _r × = . Dies führt dann aus _x,y,z:

Des weiteren gilt:

(3.6)

Es sei folgender Hinweis gegeben:

Für die Eigenzustände zu _z gilt:

Daraus erhalten wir dann das Resultat:

Wir verwenden folgenden Ansatz:

Daraus erhalten wir:

Der Drehimpuls in z-Richtung L_z ist als quantisiert (L_z-Drehimpulsquantisierung). Wir berechnen außerdem die Eigenzustände zu ² . Da [L²,L_x] = 0 gilt, existiert ein gemeinsames System von Eigenfunktionen. Wir wollen dies beweisen:

[Â,] = 0 ist die notwendige Bedingung für die Evidenz eines Systems gemeinsamer Eigenfunktionen. Wir notieren uns die Eigenwertgleichung:

sei Eigenwert von : Wir machen einen Separationsansatz:

Für die Schrödinger-Gleichung des isotropen Rotators gilt:

Daraus ergibt sich dann:

Damit erhalten wir folgende Differentialgleichung für ():

Wir machen die Substitution = cos mit -1 < < 1. Damit geht () über in F().

Der Kosinus ist außerdem sinnvoll, da es sich um eine monotone Funktion für 0 < < handelt. Wir erhalten eine Differentialgleichung für F():

Für den Spezialfall m = 0 erhalten wir die Legendresche Differentialgleichung:

Bei = ±1 darf F() nicht singulär sein. Wir machen den Reihenansatz, wobei wir dann erhalten, daß die Lösung nur für = n(n + 1), n = 0, 1, 2, ... existiert.

Durch Einsetzen in die Differentialgleichung ergibt sich:

Dann erhält man weiter:

Wir machen also einen Koeffizientenvergleich:

Daraus folgt die Rekursionsbeziehung:

Asymptotisch für k erhalten wir:

Wir führen einen Vergleich mit der Taylorreihe von f() durch:

Daraus folgt:

Physikalisch gilt für die gesuchte Wellenfunktion :

Dies führt zu einem Widerspruch, da für die asymptotische Lösung gilt:

Infolgedessen muß die Reihe abbrechen, damit wir physikalisch sinnvolle Lösungen erhalten. Dies ist nun dann der Fall, wenn der Zähler des Bruches in der Rekursionsformel gleich Null ist, womit sich ergibt;

Die Lösungen der Gleichung sind die sogenannten Legendreschen Polynome. Wir notieren uns einige dieser Polynome:

Allgemein kann man folgende Beziehung zur direkten Berechnung der Polynome herleiten:

Außerdem gilt P_l(1) = 1, was eine interessante Eigenschaft ist. Für m0 befindet sich in der Differentialgleichung ein m²; das Vorzeichen spielt also keine Rolle mehr. Macht man nun einen Reihenansatz, so erhält man eine dreigliedrige Rekursionsformel. Hier ist es dann hoffnungslos, eine Lösung zu erhalten, da die Reihe nicht abbricht. Es handelt sich dann nachweislich um kein Polynom. Eine geschlossene Form ist des weiteren ist angebbar. () ist eine Funktion von cos und sin = .

Man erhält dann folgende Differentialgleichung für P():

Wir machen einen Reihenansatz und stellen die Forderung nach nicht singulärem Verhalten. P() ist dann ein Polynom. Für m = 0 gilt wieder:

Durch Differentiation folgt:

Es handelt sich um die Differentialgleichung zu |m| = 1.

P_l() sind die Legendre-Polynome. Außerdem sind die Eigenwerte aufgrund der Isotropie des Problems nicht von m abhängig.

P0() = 1	P1() =	P2() = 2 -
	P12() = 1	P21() = 3
		P22() = 3

Dann erhält man für die Kugelflächenfunktionen:

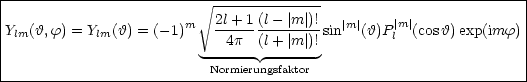
Das Vorzeichen ist Konvention. Diese Funktionen sind orthonormal:

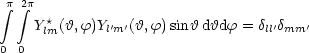
Außerdem gilt die Vollständigkeitsrelation:

l	m
0	0	Y 00(,) =
1	0	Y 10(,) = cos
	±1	Y 1,m = ±sinexp
2	0
	±1
	±2

3.8.1 Entartung

Es handelt sich um simultane Eigenfunktionen von L_x, L_y und L_z zum Eigenwert Null. Für l = 1 gilt:

Da = 0 folgt dies.

• ist Eigenfunktion zu ² mit dem Eigenwert ²l(l + 1).
• _xY _lm(,) ist aber im allgemeinen nicht Eigenfunktion zu _x.

Für l = 1 folgt:

Es handelt sich um eine Linearkombination von l = 1 zu m = ±1. Allgemein gilt: