3.7 Virtuelle Energieniveaus bzw. quasi-gebundene Zustnde

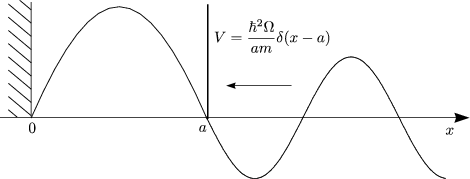
Für x > a folgt daraus eine Wellenfunktion, die man beschreiben kann durch:

i i Y(x) = sin(kx+ d) = - 2 exp (id).exp(ikx) + 2 exp (- id).exp (- ikx)

Für 0 < x < a folgt:

h2k2 Y(x) = A sin(kx) mit Ek =---- 2m

Wir fordern die Stetigkeit von (x):

A sin(ka) = sin(ka+ d)

Die Ableitung besitzt einen Sprung:

' 1 _O_ Y (a) = -2k [cos(ka+ d)+ A cos(ka)]+ a-Asin(ka) = 0

Nach langer Rechnung folgt:

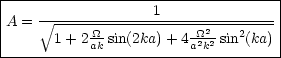
|----------------------------------| | ---------------1-------------- | A = V~ -----_O_------------_O_2---2---- | ------1-+-2ak sin(2ka)+-4a2k2 sin-(ka)-

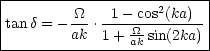
|-------------------------| | _O_-- -1--cos2(ka)--| |tan d = - ak .1+-_O_ sin(2ka)| ----------------ak---------

Für nahezu undurchdringliche Wälle ist » 1. Ist ka nicht in der Nähe von n (n = 0, 1, 2, ...), so ergibt sich A 0.