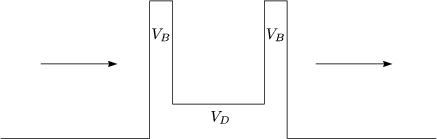

Der Einfachheit halber betrachten wir als Potential eine ![]() -Funktion. Die Barriere
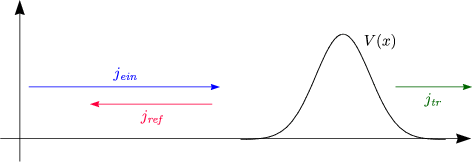
nimmt keine Energie auf. Die Streuung ist somit elastisch. Wir können dies durch
stationäre Zustände beschreiben. Die stationäre Schrödinger-Gleichung dazu
lautet:
-Funktion. Die Barriere
nimmt keine Energie auf. Die Streuung ist somit elastisch. Wir können dies durch
stationäre Zustände beschreiben. Die stationäre Schrödinger-Gleichung dazu
lautet:
Wir machen zuvor einen Einschub über die Analytizität der Lösung der
Schrödinger-Gleichung. Dazu schreiben wir diese um. Wir trennen die Anteile, in
denen die Ableitung von ![]() und
und ![]() selbst vorkommt:
selbst vorkommt:
Wir betrachten hierbei folgende Fälle:
Daraus ergibt sich dann, daß ![]() (x) und natürlich aus
(x) und natürlich aus ![]() '(x) stetig
differenzierbar ist.
'(x) stetig
differenzierbar ist.
![]() (x) muß hierbei differenzierbar sein.
(x) muß hierbei differenzierbar sein. ![]() '(x) muß stetig sein und einen
Knick haben.
'(x) muß stetig sein und einen
Knick haben.
Dieser Fall führt auf die inhomogene Schrödingergleichung.
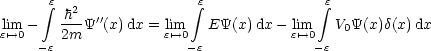
Damit erhalten wir:
![]() (x) muß somit stetig sein und
(x) muß somit stetig sein und ![]() '(x) einen Sprung haben.
'(x) einen Sprung haben.
Wir erhalten als allgemeine Lösungen:
![]() (x) ist stetig in x = 0. Damit folgt also:
(x) ist stetig in x = 0. Damit folgt also:
![]() '(x) hat an der Stelle 0 einen Sprung, womit gilt:
'(x) hat an der Stelle 0 einen Sprung, womit gilt:
Wir betrachten den Grenzfall D = 0 mit den freien Parametern k, V 0, A. Dann ergibt sich
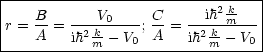
Wir erhalten folgenden Transmissionskoeffizienten:
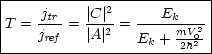
Außerdem gilt für den Reflexionskoeffizienten:
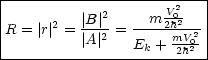
Infolge der Teilchenerhaltung resultiert die Beziehung T = 1 - R.
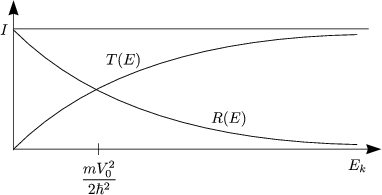
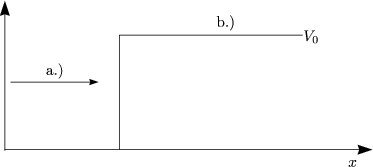
Die Schrödinger-Gleichung lautet:
Die Lösung muß von der Form exp![]() sein.
sein.