3.5 Linearer harmonischer Oszillator

Wir betrachten stationäre Zustände:

Für den Hamilton-Operator gilt mit V (x) = Dx² = m²x²:

Für die Energie-Eigenwerte ergibt sich dann:

Für die Wellenfunktionen erhalten wir:

ist die charakteristische Länge des Oszillators. H_n() sind die sogenannten Hermite-Polynome, die definiert sind durch:

Hier folgen einige Beispiele:

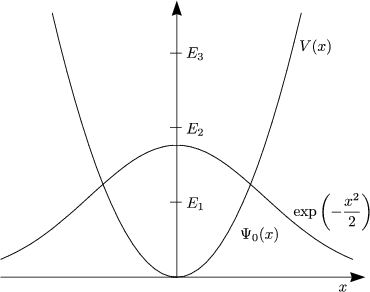
Wir betrachten folgendes Eigenwertproblem:

Für die Randwerte muß (±) = 0 gelten, also somit:

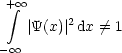
Wir gehen nun der Übersichtlichkeit halber zu dimensionslosen Größen über:

Also erhalten wir:

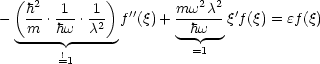
Damit folgt die dimensionslose Gleichung:

Welche sind zulässig? Wir vermuten, daß > 0 ist. Die Eigenwerte sind immer größer als der kleinste Wert des Potentials.

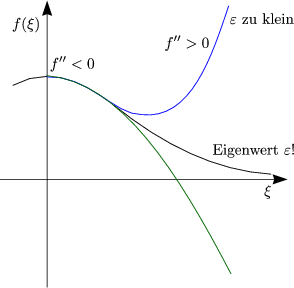
Jetzt weiß man, wir die Lösung graphisch auszusehen hat. Wir versuchen nun die Asymptotik für ± herauszufinden:

Näherungsweise gilt also:

Wir berechnen wir Ableitungen:

Asymptotisch stimmt dies also. Wir machen deshalb den Ansatz:

Die Differentialgleichung für H() lautet also, wie man durch Einsetzen von f() verifiziert:

Durch Zufall haben wir sogar eine Lösung gefunden. exp ist Lösung des Eigenwertproblems zu = 1. Die erhaltene Differentialgleichung sieht nun aber komplizierter aus als die ursprüngliche! Zur Lösung machen wir einen Potenzreihenansatz:

Durch Einsetzen und Koeffizientenvergleich erhält man folgende Rekursionsformel:

Durch den Potenzreihenansatz zerfällt die Lösung in zwei unabhängige Teilreihen.

• Gerade Funktionen:

• Ungerade Funktionen:

Dies ist sinnvoll, weil das Fundamentalsystem aus zwei linear unabhängigen Lösungen bestehen muß. Es handelt sich um eine zweigliedrige Rekursionsformel. Für k gilt:

Die geraden Lösungen schreiben wir in folgender Form:

Damit gilt:

Welche Reihe verhält sich so? Es handelt sich um die Reihenentwicklung für die Exponentialfunktion:

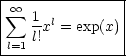
Es gilt nämlich:

Wir nehmen nun an, sei eine ungerade Zahl, also gelte = 2n + 1 mit n = 0, 1, 2, .... Genau dann bricht nämlich unsere Rekursion ab! Wir erhalten somit die Hermite-Polynome. Was jetzt noch zu zeigen wäre, ist die Orthogonalität der Eigenfunktionen zu verschiedenen Eigenwerte, das heißt mn. Wir schreiben hierzu die Differentialgleichung für die Wellenfunktion hin für die Eigenwerte n und m:

Durch Subtrahieren beider Gleichungen folgt:

Dies können wir umschreiben zu:

Durch Integration folgt nun:

Probleme:

• Problem 1:

  Wir betrachten den stationären Zustand eines harmonischen Oszillators:

  

  Wir haben die stationäre Schrödingergleichung:

  

  Daraus ergibt sich dann:

  
  

  Überlagerungen von stationären Zuständen sind im allgemeinen nicht stationär. Wir führen das Beispiel auf dem Übungsblatt an:

  

• Problem 2:

  Es gilt folgende Beziehung:

  

  Wir ersetzen die Wellenfunktion durch ihre Fouriertransformierte. Wir zerlegen also in die Impulseigenfunktionen:

  

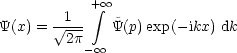
  Wir berechnen den Erwartungswert:

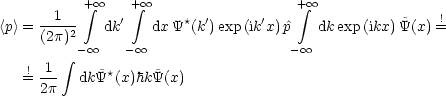  (3.2)

  Wir raten den Ansatz = a und vergleichen:

  (3.3)

  Daraus ergibt sich dann durch Vergleich mit oben:

• Problem 3:

  Wir betrachten folgende Integrale:

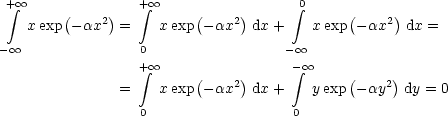  (3.4)

  

Wenn ich den Erwartungswert einer Observablen ausrechnen möchte, mache ich dies durch:

Die Wahrscheinlichkeit hängt natürlich sowohl von der Observablen als auch vom Zustand ab, in dem ich mich befinde.

Die Ortswahrscheinlichkeit ist gegeben durch das Betragsquadrat der Wellenfunktion im Ortsraum:

Für die Impulswahrscheinlichkeit folgt:

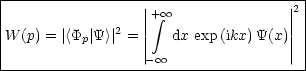
Damit W als Wahrscheinlichkeitsdichte aufgefaßt werden kann, muß gelten:

Die Gesamtwahrscheinlichkeit muß also gleich Eins sein. Für die Ableitung der Gesamtwahrscheinlichkeit muß verschwinden:

Wenn dies nicht so ist, passiert irgendetwas von außen mit dem System. Wenn wir ein kontinuierliches Spektrum haben, so folgt:

Dies kann man nun umschreiben, indem man die Ableitung vor der Integration ausführt:

Dazu betrachten wir die Schrödingergleichung:

Für die komplex konjugierte Wellenfunktion ^* gilt auch:

Der Hamilton-Operator ist hermitesch. Durch Multiplikation der ersten Gleichung mit ^* und der zweiten mit und anschließender Addition erhalten wir:

Durch Einsetzen haben wir dann:

Die Gesamtwahrscheinlichkeit ist somit zeitunabhängig.

Der lokale Erhaltungssatz (wie in der Elektrodynamik für Q) erhalten wir durch:

Daraus folgt:

Es gilt nun folgende Operator-Identität:

Es handelt sich hier um die Kontinuitätsgleichung.

3.5.1 Einschub: Parität und Paritätsoperator

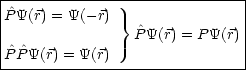
Man unterscheidet also:

• Ungerade Parität

• Gerade Parität

Satz:

Beispiel: Linearer harmonischer Oszillator

Daraus ergibt sich:

Also gilt:

3.5.2 Wahrscheinlichkeitsstromdichte

Daraus ergibt sich dann für die Wahrscheinlichkeitsstromdichte mit p = k und = v:

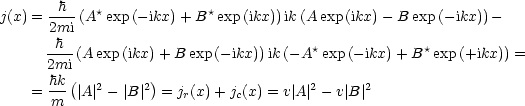(3.5)

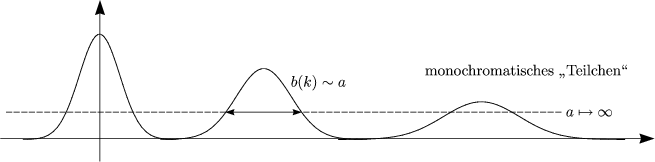
Ein Teilchenstrahl läßt sich sinnvoll durch ebene Welle beschreiben.