[next] [prev] [prev-tail] [tail] [up]

3.4 Teilchen im „Kasten“

PIC

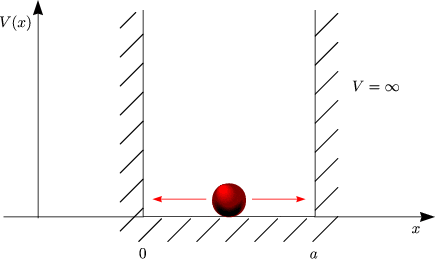
Es gilt für den Hamilton-Operator innerhalb des Kastens:

h2 @2 H^= - -----2-f¨ur 0 < x < a 2m @x

Für die Wellenfunktion gelte am Rand:

Y(x) = 0 f¨ur x = 0, a

Ein hermitescher Operator ist ein solcher, den man sowohl auf rechts als auch auf links anwenden kann:

| integral -----[------]------ integral -[-----]----------------| | Y*1(x) G^Y2(x) dx = ^GY1(x) *Y2(x) dx A Yn(x)| -------------------------------------------------

Wenn Y1 = Y2 reell sind, so sind auch die Eigenwerte reell. Durch partielle Integration folgt:

integral [ ] integral Y* (x) -i@Y2(x)- dx = [Y* (- iY (x))]a- (-iY (x)) @Y*1dx 1 @x 1 2 0 2 @x

Wenn die Wellenfunktion am Rande gleich Null ist, so fällt der Oberflächenterm heraus, womit folgt:

integral * integral [ ]* [Y*(- iY2(x))]a - (- iY2(x)) @Y1-dx = -i@Y1- Y2(x)dx 1 0 @x ---@x--- ^pY1

Aufgrund der Randbedingungen kann es sich bei der Wellenfunktion nur um eine Sinusfunktion handeln:

Y (x) = B sin(kx) n

Somit erhält man nach einer Normierung für n = 1, 2, ...:

|-------- V~ ----(----)-| |Yn(x) = 2sin np-x | -----------a-----a----|

|---------------| | -h2(np-)2 | -En-=-2m---a----|

PIC

PIC

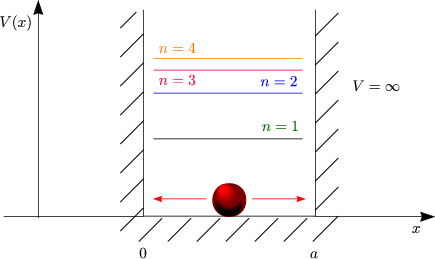
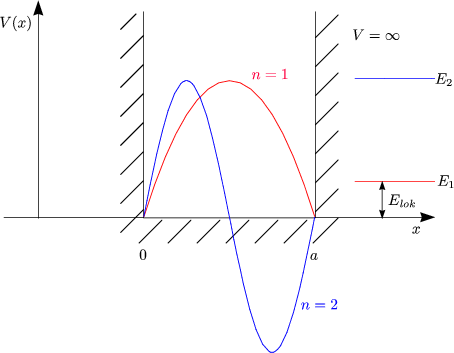
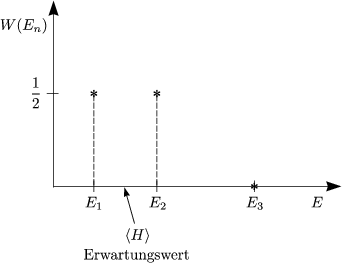
Die Lokalisierungsenergie (Nullpunkt: En)

h2p2- Elok = 2ma2 > Energie in Coulombpotential

Für zwei geladene Teilchen haben wir folgendes Coulombpotential:

2 V = --1- .e- 4pe0 r

Dies gewährleistet die Stabilität der Materie.
Die Wellenfunktionen zu verschiedenen Energien sind orthogonal:

integral * Y m(x)Ym(x) dx = 0 f¨ur m /= n

Beweis-Idee:
Es gilt:
sin(mq) .sin(nq) = 1[cos(m -n) q- cos(m + n)q] mit q = px 2 a

Durch Integration folgt dann obigen Orthogonalität.

Erwartungswerte:
Mittels BRONSTEIN oder durch direkte Rechnung folgt dann:
integral * a <x> = Yn(x)xYn(x)dx = 2-

integral ( ( ) ) 2 * 2 a2 3 1--2 <x > = Yn(x)x Yn(x)dx = 3 1- 2 . np

Dann folgt für die Streuung:

[ ] 2 1- ---1-- 2 (Dx) = 12- 2(pn)2 a

integral * ( -@-) <p> = Y n(x) -ih@x Yn(x) dx = 0

Dies ist natürlich so, weil der Impuls als physikalische Größe reell sein muß!

integral ( @ )2 (np )2 <p2> = Y*n(x) - ih --- Yn(x)dx = h2 --- @x a

Außerdem zeigen wir, daß für dieses Beispiel die Unschärferelation gilt:

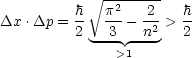
V~ -------- Dx .Dp = h- p2-- 2- > h- 2 --3 --n2 2 >1

3.4.1 Orts-Wahrscheinlichkeitsdichte

integral integral <x > = Y*(x).xY(x) dx = WX(x) .xdx

Damit haben wir also:

|-------------| |W (x) = |Y(x)|2| ---------------

PIC

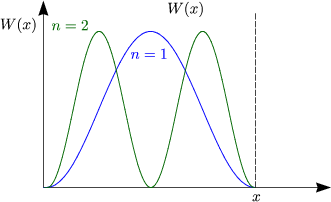
Dies ist die „Aufenthaltswahrscheinlichkeit“ des Teilchens.

3.4.2 Impuls-Wahrscheinlichkeitsdichte

integral integral <p> = W (p).pdp = Y*(x)G^Y(x) dx

Wie kann man jetzt W(p) berechnen? Allgemein gilt für kontinuierliche g:

integral <G > = W (g).g dg

Für diskrete g gilt:

<G > = sum W (g ).g n n n

Wir entwickeln Y(x) = sum nCnfn(x):

integral ^Gfn(x) = gnfn(x), f*mfn dx = dmn

^ sum 2 <G> = |Cn |.gn n

Man erhält somit die Wahrscheinlichkeitsdichte, einen bestimmten Eigenwert Cn zu finden:

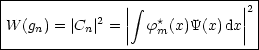
|-------------------------------| | || integral ||2| |W (gn) = |Cn |2 = || f*m(x)Y(x)dx|| | ---------------------------------

Somit gilt für die Eigenfunktionen des Impulses:

^pfk(x) = hkfk(x)

Wir normieren die Impulswellenfunktionen auf d-Funktionen:

f (x) = V~ -1-exp(ikx) k 2p

k ist hierbei die Impulsquantenzahl, für die - oo < k < oo gilt (Impuls: hk).

integral f*k(x)fk(x)dx = d(k - k')

d-Funktionen sind nichts weiteres als die Verallgemeinerung des Kronecker-Deltas. Wir entwickeln unsere Wellenfunktion nach ebenen Wellen:

integral Cn '--> C(k) = f*k(x)Y(x) dx

Dies ist also die Fouriertransformierte der Wellenfunktion. Für die Impulswahrscheinlichkeit erhält man:

W (p) = |C(k)|2 mit p = hk

PIC

3.4.3 Überlagerung zweier stationärer Zustände

Y(x) = N (Y1(x) + Y2(x))

Diese Wellenfunktion ist keine Lösung der stationären Schrödingergleichung:

^HY = EY

Es gilt nämlich E1/=E2!

( ( ) ( )) Y(x,t) = N Y1(x) exp - iE1-t + Y2(x) exp - iE2-t h h

Per Konstruktion ist dies eine Lösung der zeitabhängigen Schrödingergleichung. Man muß die Funktion noch normieren:

integral |Y(x,t)| 2dx = 1

Daraus folgt N = V~ 1 2, da Y1,2 normiert und orthogonal sind. W(x,t) = |Y(x,t)|2 ändert sich zeitlich.

[ [ ( ) ( )]] ( ) |Y(x,t)| 2 = 1 |Y (x)| 2 + |Y (x)| 2 + Y (x)Y (x) exp iE2--E1-t + exp -iE2---E1t = ...cos E2---E1t 2 1 2 1 2 h h h

Die Frequenz des oszillierenden „Wellenpakets“ist:

|-----------| | E2- E1 | |w = --h----| -------------

Wir groß ist die Wahrscheinlichkeit, einen bestimmten Wert der Energie bei einer Messung zu finden?

PIC

2 W (En) = |Cn|

sum Y(x) = Cnfn(x) n

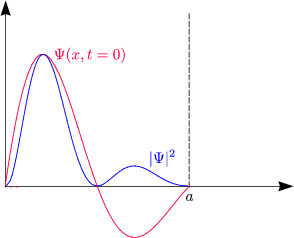
Man muß eine Wellenfunktion nach den Eigenfunktionen entwickeln, nach deren Wahrscheinlichkeit man fragt. Unsere Wellenfunktion ist schon in Eigenfunktionen zerlegt. Deshalb lesen wir direkt ab:

1 ( E1t) C1 = V~ -exp - ih- 2

-1- ( E2t) C2 = V~ 2-exp - ih

C3 = C4 = ...= 0

PIC

Die Verteilung ist zeitlich konstant, obwohl Y(x,t) gilt. Aus dem Energieerhaltungssatz folgt, daß <^H>, DH, ... zeitlich konstant sind. Allgemein gilt für G^:

d < > d + integral oo integral ([@Y ]* @G^ @Y ) -- Y(x,t)| ^G(^p,^x,t)| Y(x,t) = -- Y*(x,t)G^(^p,^x,t)Y(x,t)dx = --- G^Y + Y*---Y + Y*^G --- dx dt dt- oo @t @t @t

Aufgrund der hermiteschen Eigenschaften haben wir:

d < > integral ( i[ ]* @ ^G ( i) ) -- Y(x,t)|G^(^p,x^,t)| Y(x,t) = --H^Y (G^Y) + Y* ---Y+ Y*^G - -- ^HY dx = dt h [ @t ] h integral @ ^G i[ ] = Y*(x,t) @t-+ h- ^H .^G - ^G .^H Y(x,t)dx
(3.1)
Wir nennen ^HG^-^G^H den Kommutator [ ] H^, ^G. Analog zur klassischen Physik gilt dann mittels der Poisson-Klammern:
dG^ @ ^G i-[^ ^] @G^ dt = @t + h H,G = @t +{H, G}

Wir haben folgende kanonische Variable:

{p,x}= 1 '--> [p^,^x] = - ih

Dann gilt nach der Produktregel:

@ @f (x) [^p,x]f (x) = -ih@x-[xf(x)]- x(- ih)--@x- = -ihf(x)

Der Hamilton-Operator H^ hängt nicht (explizit) von der Zeit t ab.

[H^, ^H] = 0

Das heißt, daß ^H erhalten ist.

3.4.4 Ortseigenzustände

q sei der Eigenwert zum Ortsoperator ^x.
^xYq(x) = qYq(x)

Y (x) = d(x - q) q

Diese Funktionen Y sind auch auf d-Funktionen normierbar.

integral Y*(x)Y '(x)dx = d(q- q') q q

[next] [prev] [prev-tail] [front] [up]