[next] [prev] [prev-tail] [tail] [up]

3.3 Freies Teilchen

Es gilt für den Hamilton-Operator und Impuls-Operator:

|--------||---------------| |^H = -^p2 ,p^= -ih-@-, ^x = x -----2m--|-------@x--------

Für den Eigenzustand des Impulses erhalten wir:

^pf(x) = hkf(x)

hk ist der Impuls-Eigenwert.

@f- - ih@x = hkf(x)

' f (x) = ikf(x)

Damit erhält man:

|-----------------| |fk(x) = Akexp (ikx)|f¨ur- oo < k < oo -------------------

Die Wellenfunktion ist leider nicht normierbar:

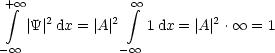
+ integral o o oo integral |Y|2dx = |A|2 1dx = |A|2 . oo = 1 - oo - oo

Den Ausweg findet man durch Einführung eines Normierungsvolumens V :

|-------| | -1-| A = V~ V| ---------

Man führt die Normierung auf d-Funktionen durch:

integral <fk|fk'= f*(x)fk'(x)dx = d(k - k') (xdkk“) k

Dies ist erfüllt durch:

-1-- fk(x) = V~ 2p-exp(ikx)

Man kann dieses Funktionssystem verwenden, um Wellenpakete aufzubauen:

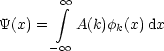
oo integral Y(x) = A(k)f (x)dx k - oo

integral |Y |2dx = 1

Wie sehen die Eigenzustände (stationäre Zustände) zu H^ aus? Die Eigenzustände von ^p sind auch Eigenzustände von ^H mit der Energie Ek:

|-----h2k2| |Ek = ----| ------2m---

Wir lösen das Problem direkt für den Hamilton-Operator H^:

h2-@2f- h2k2 - 2m @x2 = 2m f(x)

Dann erhalten wir einen alten Bekannten, nämlich die Gleichung für den Harmonischen Oszillator:

f''(x)+ k2f(x) = 0

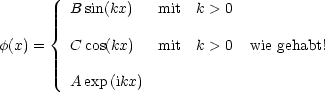
Bsin(kx) mit k > 0 { f(x) = Ccos(kx) mit k > 0 wie gehabt! Aexp (ikx)

Man erhält die Zeitabhängigkeit dann durch:

( ) Bsin(kx).exp - iEkt h ( ) f(x,t) = { Ccos(kx).exp -iEkt mit w = Ek-, hw = E h h k ( ) Aexp ikx- Ekt- h

[next] [prev] [prev-tail] [front] [up]