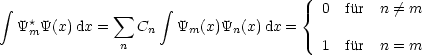 (x) sei eine komplexe Funktion, die folgendermaßen normiert ist: |
|(x)|2 dx = 1 |
| Einer physikalischen Größe (Observable) G wird ein lineare (hermitescher) Operator zugeordnet: |
G  : (x)  (x) =  (x) |
| In der Mathematik nennt man dies eine Abbildung. |
| Hierbei gelten die Übersetzungsregeln: |
x  = x |
p  = -i  |
G  = Gklass( ,  ) |
| Man erhält den Wert einer Größe G folgendermaßen: |
W(Z;G) =
*(x) dx = <| |> =  |
| Mathematisch handelt es sich hier um das Skalarprodukt. Ein Operator ist nun immer so zu verstehen, daß dieser nach rechts wirkt. |
Dynamik: Es sei (x) zur Zeit t = t0 gegeben, dann gelte also  (x,t). Dann gilt:
|
= 
= 
+ 
) = 
+ 3.2.1 Physikalisch relevante Zustände
Stationäre Zustände sind Zustände der Ruhe! Alle physikalischen Größen haben zeitlich konstante Werte.
Durch Einsetzen fällt die t-Abhängigkeit heraus:
![[ ]
ih(- iw)Y(x) exp (-iwt) = ^HY(x) exp(-iwt)](th149x.gif){kind=small}
Dann erhält man schließlich:
Es handelt sich um ein Eigenwertproblem für die Energie. Man nennt diese auch im Fachjargon „Stationäre Schrödinger-Gleichung“. Es gibt mehrere Zustände, die stationäres Verhalten zeigen. Diese bezeichnen wir dann mit dem Index n:
- Es gibt unendlich viele 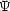n(x), En
- Beliebige 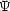(x) lassen sich linearkombinieren:
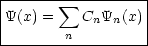
Was man in der Natur in Form von Spektrallinien findet, manifestiert sich in „Sprüngen“zwischen solchen stationären Zuständen.
Welches sind die Zustände Z, in denen eine Größe 
einen scharfen Wert
besitzt, d.h. 
G = 0 gilt?
Dann erhält man auch wieder ein Eigenwertproblem für den Operator
:
Im allgemeinen gilt es davon immer unendlich viele:
Die n, m zu gn
gm sind „orthogonal“, also gilt:
Die Menge der Eigenfunktionen n(x) ist vollständig, d.h.
Jede Funktion ist somit nach n(x) entwickelbar (Eigenwerte einfach). Wie
berechnet man nun die Cn’s? Man multipliziert dazu die Gleichung mit
m:
