2.4 Klassische Wellen (Felder, mit Blick auf Quantenmechanik)
Ein Feld ist ein physikalisches System mit räumlich verteilten Größen. Man
unterscheidet:
2.4.1 Wellengleichung
Diese lautet für eine erregende (äußere) Kraft f(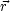 ,t):
,t):
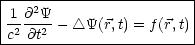
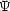 (
(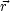 ,t) beschreibt eine Komponente von
,t) beschreibt eine Komponente von 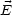 und
und 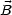 . Die Diffusionsgleichung hat
beispielsweise auch Ähnlichkeit mit der Wellengleichung, allerdings enthält sie nur
eine erste zeitliche Ableitung:
. Die Diffusionsgleichung hat
beispielsweise auch Ähnlichkeit mit der Wellengleichung, allerdings enthält sie nur
eine erste zeitliche Ableitung:
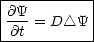
Auch die Schrödingergleichung für ein freies Teilchen ist eine Wellengleichung:
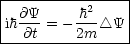
Der Zustand der Wellengleichung ist durch Kenntnis von 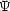 (x,t) bei t = t0 und
(x,t) bei t = t0 und
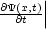 t=t0 festgelegt. Dies entspricht Ort und Geschwindigkeit aus der Mechanik.
Wenn man die Größen kennt, die den Zustand festlegen, kennt man somit alle Größen
des Systems. Die allgemeine Lösung der Wellengleichung enthält zwei freie
Konstanten a, b, also zwei freie Funktionen f(x), g(x), die an jedem x verschieden
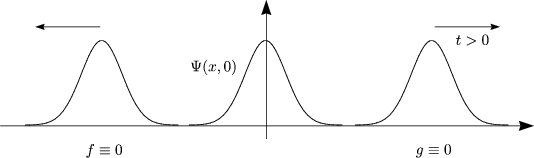
sein können! Die allgemeinste Lösung in einer Dimension ist von folgender
Form:
t=t0 festgelegt. Dies entspricht Ort und Geschwindigkeit aus der Mechanik.
Wenn man die Größen kennt, die den Zustand festlegen, kennt man somit alle Größen
des Systems. Die allgemeine Lösung der Wellengleichung enthält zwei freie
Konstanten a, b, also zwei freie Funktionen f(x), g(x), die an jedem x verschieden
sein können! Die allgemeinste Lösung in einer Dimension ist von folgender
Form:
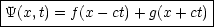
2.4.2 Wellenpakete
Für eine monochron (ebene) Welle erhalten wir folgende
Beschreibung:
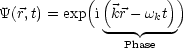
Ebenen sind in diesem Falle Ort konstanter Phasen. Ein Wellenpaket erhält man
nun durch Superposition von ebenen Wellen:
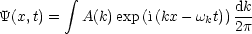
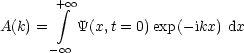
Das Charakteristikum von Wellen ist, daß sie durch eine Beziehung zwischen  und
k, nämlich der sogenannten Dispersionsrelation, beschrieben werden:
und
k, nämlich der sogenannten Dispersionsrelation, beschrieben werden:
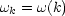
Für elektromagnetische Wellen im Vakuum gilt beispielsweise:
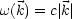
Wenn man Wellenphänomene hat, welche durch eine lineare Gleichung beschrieben
werden, bereitet sich das Wellenpaket formstabil aus:
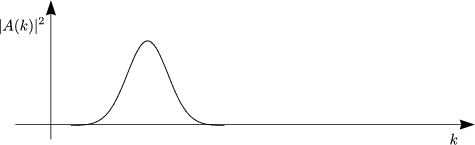
Man unterscheidet nun:
- Gruppengeschwindigkeit:

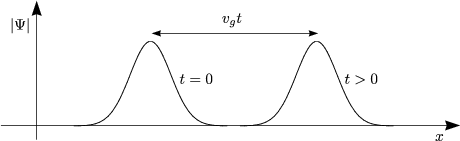
- Phasengeschwindigkeit:
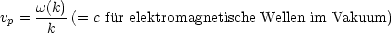
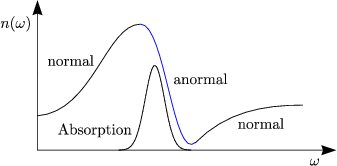
Bei elektromagnetischen Wellen in Materie haben wir folgenden Brechungsindex
n( ):
):
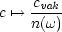
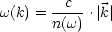
Die Form des Wellenpakets ändert sich bei der Ausbreitung;

Man unterscheidet außerdem zwischen:
- Normale Dispersion:
Dies bedeutet, daß der Brechungsindex mit der Frequenz zunimmt.
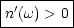
- Anormale Dispersion:
Der Brechungsindex nimmt mit der Frequenz ab.
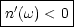
Des weiteren gilt die „Unschärfe-Relation“ für x und k:

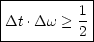
Die Zahlen auf der rechten Seite der Ungleichungen hängt von der Definition der  ’s
ab. Wir definieren das Betragsquadrat als „Intensität“:
’s
ab. Wir definieren das Betragsquadrat als „Intensität“:
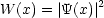
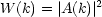
Auch hier können wir die Erwartungswerte bilden:
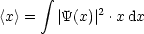
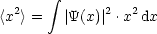
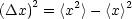
Die Folgende Relation nennt man Parsevalsche Gleichung:
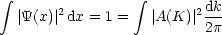
Wir wollen diese kurz beweisen:
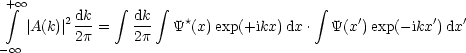
Außerdem gilt:
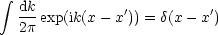
Womit wir dann erhalten:
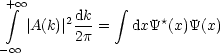
![integral integral integral integral
|A(k)|2 .kdk-= dkk Y*(x)exp(ikx)dx Y(x')exp(-ikx')dx'=
2p integral 2p integral [ integral ]
= dx dx' k exp(ikx).exp(-ikx')dk Y*(x)Y(x)](th95x.gif) | (2.1) |
Für den Ausdruck in der Klammer gilt:
![integral @ [ integral ]
k exp(ikx).exp(-ikx')dk = i--' exp(ikx) .exp(- ikx')dk
@x](th96x.gif)
Somit erhalten wir wieder die  -Funktion:
-Funktion:
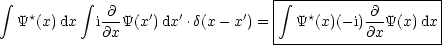
Man erhält den Impuls, indem man die Wellenfunktion fouriertransformiert. Nach de
Broglie gilt:
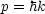
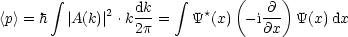
Folgenden Ausdruck bezeichnet man nun als Impulsoperator:
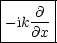
2.4.3 Beweis der Unschärfe-Relation (Pauli)
Wir werden nun einen Beweis
kennenlernen, der etwas undurchsichtig sein mag. Wir notieren uns hierzu als
allererstes eine Relation, die auf jeden Fall gilt, da der Betrag einer komplexen
Funktion immer positiv ist:
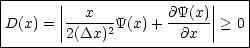
Dies ist nichts anderes als die Schwarzsche Ungleichung für Vektoren. Durch
Quadrieren und integrieren folgt:
![integral integral [ ( )]
D2(x)dx = --x2--Y*Y + @Y*-@Y-+ ---x-- Y @Y*-+ Y*@Y- dx =
4(Dx)4 @x @x 2(Dx)2 @x @x
---1-- integral 2 2 integral @Y*-@Y ---1-- integral [@--- * ]
= 4(Dx)4 x | Y |dx + @x @x dx + 2(Dx)2 x. @x(Y Y) dx > 0](th102x.gif) | (2.2) |
O.B.d.A. gilt:
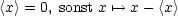

Damit gilt also nach der Fouriertransformation:
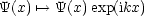
- Erster Term:
Mit <x> = 0 resultiert dann:
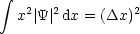
- Zweiter Term:

- Dritter Term
Mit dem letzten Term führen wir eine partielle Integration durch:
![integral [ ] integral
x. @-(Y*Y) dx = x[Y*Y] oo - 1 .|Y |2dx = - 1
@x - oo](th108x.gif)
Dadurch, daß die Wellenfunktionen im Unendlichen verschwinden müssen
und daß diese außerdem normiert sind, folgt dieses Resultat.
Damit erhalten wir also, um den letzten Term nochmals zu rezitieren:
![integral integral integral [ ]
--1--- x2| Y |2dx + @Y*-@Y-dx + ---1-- x. -@-(Y*Y) dx > 0
4(Dx)4 @x @x 2(Dx)2 @x](th109x.gif)

Wir multiplizieren mit ( x)2 durch und erhalten:
x)2 durch und erhalten:
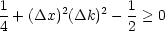

Damit erhalten wir schließlich:
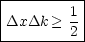
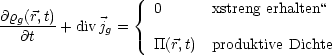
![]() .
.![]() ist die Mange an Arbeit, die mit bewegten Ladungen zusammenhängt.
Selbst wenn ein Magnetfeld im Spiel ist, steht auf der rechten Seite der
Gleichung kein B, da die Lorentzkraft ja keine Arbeit leistet.
ist die Mange an Arbeit, die mit bewegten Ladungen zusammenhängt.
Selbst wenn ein Magnetfeld im Spiel ist, steht auf der rechten Seite der
Gleichung kein B, da die Lorentzkraft ja keine Arbeit leistet.

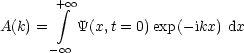




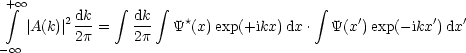
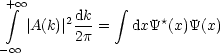
![integral integral integral integral
|A(k)|2 .kdk-= dkk Y*(x)exp(ikx)dx Y(x')exp(-ikx')dx'=
2p integral 2p integral [ integral ]
= dx dx' k exp(ikx).exp(-ikx')dk Y*(x)Y(x)](th95x.gif)
![integral integral [ ( )]
D2(x)dx = --x2--Y*Y + @Y*-@Y-+ ---x-- Y @Y*-+ Y*@Y- dx =
4(Dx)4 @x @x 2(Dx)2 @x @x
---1-- integral 2 2 integral @Y*-@Y ---1-- integral [@--- * ]
= 4(Dx)4 x | Y |dx + @x @x dx + 2(Dx)2 x. @x(Y Y) dx > 0](th102x.gif)