Wir wählen das Schrödinger-Bild und die Ortsdarstellung.
Die Basisvektoren sind orthonormiert:
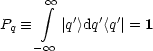
Jedes |
> wird durch die „Einspaltenmatrix“ mit „Komponenten“ <q'|> dargestellt.
<q'|>
(q') ist die Wellenfunktion. Wir bilden das Skalarprodukt von |> mit
|
>:
Wir schreiben die Funktion V (
) wirkend auf |> auf:
Hierbei handelt es sich um eine einfache Multiplikation. Ebenso gilt:
Wir betrachten den Hamilton-Operator:
Durch Einsetzen in die obige Beziehung folgt:
![[ h2 @2 ]
<q'|H^|Y > = - -----'2-+ V(q') Y(q')
2m @q](th179x.gif){kind=small}
Im Schrödinger-Bild gilt:
Daraus folgt schließlich die Schrödingergleichung:
![|------------[---------------]-------|
ih @-Y(q',t) = --h2-@2-+ V (q') Y(q',t) |
--@t-----------2m-@q'2----------------](th181x.gif){kind=small}
Ebenso gilt dies in der {p}-Darstellung:
Daraus folgt dann auch hier die Schrödingergleichung:
