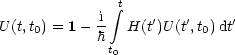4.5 Quantentheorie
4.5.1 Zustände und Messungen
Zu jedem Zustand eines Quantensystems gehört
ein bestimmter |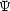 > des Hilbertraums E. Jeder dynamischen Variablen wird eine
Observable des Raumes E zugeordnet. Es gibt drei Grundpostulate:
> des Hilbertraums E. Jeder dynamischen Variablen wird eine
Observable des Raumes E zugeordnet. Es gibt drei Grundpostulate:
- Wahrscheinlichkeitspostulat:
Wir haben eine physikalische Größe A verknüpft mit der Funktion F.
Dann nennen wir <F(A)> = <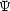 |F(Â)|
|F(Â)|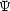 > den Erwartungswert.
> den Erwartungswert.
- Messungspostulat:
- Die einzigen Werte, welche die Größe A annehmen kann, sind die
Eigenwerte der Observable Â.
- Die Wahrscheinlichkeit WD dafür, daß das Meßergebnis zum Bereich
D des Spektrums gehört, ist gegeben durch:
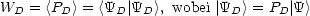
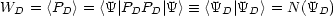
- Das Postulat der „Reduktion des Wellenpakets“:
Ein System befinde sich im Zustand |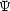 >. Eine Idealmessung ergebe das
Resultat D. Durch das Eingreifen in das Experiment ergibt sich ein neuer
Zustandsvektor:
>. Eine Idealmessung ergebe das
Resultat D. Durch das Eingreifen in das Experiment ergibt sich ein neuer
Zustandsvektor:
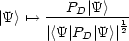
Beispiel:
Wir nehmen an, daß D ein Eigenwert a1 des diskreten Spektrums ist.
Also gilt die Eigenwertgleichung:

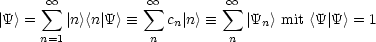
Die Wahrscheinlichkeit W1, um für A den Wert a1 zu finden, berechnet sich nun
nach:
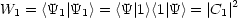
Wenn ich nun a1 gemessen habe, verändert sich die Situation:
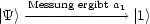
4.5.2 Bewegungsgleichungen („Reduktion des Wellenpaktes“)
Ein isoliertes
System ist deterministisch. Zur Zeit t0 sei ein Vektor |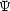 (t0)> und zur Zeit t ein
Vektor |
(t0)> und zur Zeit t ein
Vektor |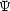 (t)> = U(t,t0)|
(t)> = U(t,t0)|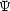 (t0)> gegeben. U(t,t0) nennt man Entwicklungsoperator.
Wir postulieren:
(t0)> gegeben. U(t,t0) nennt man Entwicklungsoperator.
Wir postulieren:
Daraus folgt dann das vierte Quantenpostulat (Postulat 4(S)), nämlich die
Schrödingergleichung:
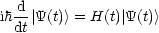
![[ d ]
ihdtU (t,t0)Y|(t0) > = [H(t)U(t,t0)]| Y(t0)> = H(t)| Y(t)>](th136x.gif)
Wir machen einen kleinen „Zeitsprung“:
![[ ]
' i- ' '
|Y(t + dt)> = 1- hH(t )dt |Y(t )>](th137x.gif)
Daraus folgt dann:
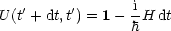
Wir wollen zeigen, daß der Operator unitär ist:
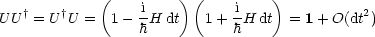
Man kann nun das Zeitintervall von t0 nach t in infinitesimal kleine Stückchen
einteilen. Dann kann U(t,t0) als Produkt geschrieben werden:
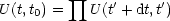
Als Produkt der unitären Operatoren U(t' + dt,t') ist auch U(t,t0) unitär.
4.5.3 Das Schrödinger-Bild
|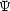 (t)> sei gegeben. Die Wahrscheinlichkeit,
(t)> sei gegeben. Die Wahrscheinlichkeit, 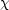 zu finden
ergibt sich dann aus:
zu finden
ergibt sich dann aus:
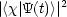
Wir wenden den Entwicklungsoperator an:
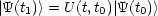
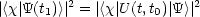
4.5.4 Das Heisenberg-Bild
Wir erhalten das Heisenberg-Bild aus dem
Schrödinger-Bild durch eine unitäre Transformation mit dem Operator U†(t,t0).
Damit ergibt sich:
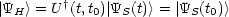
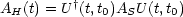
Daraus folgt die „neue Bewegungsgleichung“, also das 4.Quantenpostulat im
Heisenberg-Bild (Postulat 4(H)):
![ih dAH-= [A ,H ]+ih@AH-
dt H H @t](th146x.gif)
Man nennt diese die Heisenberg-Gleichung. Wir setzen AH(t) in diese Gleichung ein.
Dazu werten wir zuerst die Zeitableitung auf der linken Seite aus:
![d @AS @AS
ihdtAH = U†ASHSU + ihU †-@t-U - U†HASU = U †[AS,H]U + ihU†-@t-U](th147x.gif)
Mit HH = U†HU folgt:
![-d †( † † ) †@AS- @-
ihdtAH = U ASU U H - HU U AS U + ihU @t U = [AH, HH] + ih @tAH](th148x.gif)
Jeder Ket-Vektor im Heisenberg-Bild beschreibt eine mögliche Bewegung des
Systems.
Intermezzo:
Betrachten wir ein Quantensystem mit Observablen
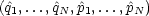 und den Kommutatorbeziehungen [
und den Kommutatorbeziehungen [ m,
m, n] = [
n] = [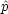 m,
m,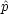 n] = 0;
[
n] = 0;
[ m,
m, n] = i
n] = i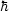
 mn. Das klassische System habe die dynamische Variable
Aklass = A(q1,...,qN) und erfülle die Bewegungsgleichung:
mn. Das klassische System habe die dynamische Variable
Aklass = A(q1,...,qN) und erfülle die Bewegungsgleichung:
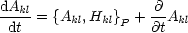
Mit der Definition der Poisson-Klammern:
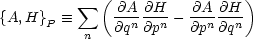
Man macht den Schritt von „Klassisch“ nach „Quantenmechanik“ durch:
![|-------------------------------------|
|{A,B}Poissonklammer '--> -1[ ^A,B^]Kommutator|
---------------------ih---------------|](th158x.gif)
4.5.5 Erwartungswerte
- Heisenberg-Bild:
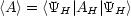
- Schrödinger-Bild:
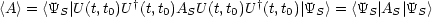
Die Erwartungswerte im Schrödinger- und Heisenbergbild sind damit gleich.
4.5.6 Das Wechselwirkungsbild
Es sei folgender Hamilton-Operator gegeben:
![[ ]
H = H(0) + H(1) mit H = H † H(0),H(1) = 0](th161x.gif)
H(1) sei klein. Wir betrachten die strenge Lösung der Schrödingergleichung:
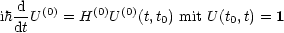
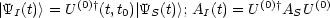
Im Wechselwirkungsbild ändern die Kets sich langsam, da H(1) klein ist:
![|--d--------------------@---|
|ih--AI(t) = [AI,H(0I)]+ ih-AI |
--dt-------------------@t----](th164x.gif)
Es gilt allgemein:
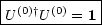
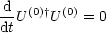
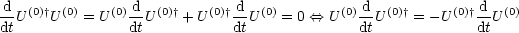
Dies wird im folgenden benötigt:
![[ ]
d- (0)† (0)† (0) d (0)† (0)† d- (0) (0)† (0)† (0) (0) (0)† (0)† 0
ihdtU = ih.U U dtU = -U ih dtU U = - U H U U = - U H](th168x.gif)
Durch Einsetzen in die Schrödinger-Gleichung unter Berücksichtigung der
Produktregel folgt dann:
![( )
ih d-U (0)†|YS> = -U (0)†H(0)|YS>+U (0)† H(0) + H(1) |YS > = [U (0)†H(1)U(0)]U(0)†| YS > = H(1)(t)|YI(t)>
dt I](th169x.gif)

Das Wechselwirkungsbild ist sehr gut geeignet zur Beschreibung von Streuprozessen.
![]() |F(Â)|
|F(Â)|![]() > den Erwartungswert.
> den Erwartungswert.
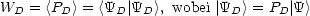
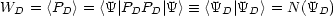
![]() >. Eine Idealmessung ergebe das
Resultat D. Durch das Eingreifen in das Experiment ergibt sich ein neuer
Zustandsvektor:
>. Eine Idealmessung ergebe das
Resultat D. Durch das Eingreifen in das Experiment ergibt sich ein neuer
Zustandsvektor: