4.4 Darstellung durch Matrizen

[next] [prev] [prev-tail] [tail] [up]

4.4 Darstellung durch Matrizen

Wir haben die Eigenwertgleichung |m> = q_m|m> mit m = 1, 2, 3, ....
Die Vektoren |k> und |l> seien normiert, also gelte <k|l> = _kl.
$sum PQ =_ |m ><m |= 1 m$
|m> sind die Basisvektoren in der {Q}-Darstellung. Für jeden Vektor |u> kann man schreiben:
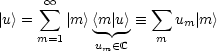
$oo |u> = sum |m ><m|u> =_ sum um |m> m=1 - - m um( - C$
Die Zahlen u_m kann man als die Elemente einer Spaltenmatrix mit dem Zeilenindex m. Der Spaltenvektor |u₁,u₂,u₃,...>definiert |u> vollständig. Ebenso kann man dies für einen Bra-Vektor schreiben:
$sum sum <v|= <v|n><n | =_ vn<n | n n$
Der Zeilenvektor stellt den Bra-Vektor <v| in der Q-Darstellung dar. Ebenso kann jeder linearer Operator Â in eine Doppelreihe entwickelt werden:
$^A = sum |m><m |A^|n><n|= sum A | m ><n| m,n -- -- m,n mn Am,n (- C$
Die A_mn können als die Elemente einer quadratischen Matrix mit Zeilenindex n und Spaltenindex m angesehen werden.
$( ) A11 A12 A13 ... A21 A22 A23 ... A = A31 A32 A33 ... .. .. .. .. . . . .$
Diese Matrix stellt den Operator Â in der Q-Darstellung dar. Man kann dies nachlesen in BORN-HEISENBERG-JORDAN, Z.Phys. 35 (1926), 537.
Erinnern wir uns an die Definition des adjungierten Operators: $( ) A †mn =_ <m |A^†| n> = <n|^A|m>*= (Anm)*$
Man muß also die Matrix A transponieren und komplex konjugieren. Wir betrachten nun ein Produkt der Operatoren Â und :
$sum sum (AB)mn = <m |A^^B|n> = <m|A|k><k|B|n> = AmkBkn k k$
Dies entspricht also gerade der Matrixmultiplikation.
Observable Q in der {Q}-Darstellung
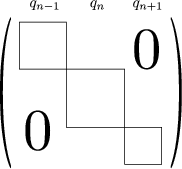
Diese wird dargestellt durch eine Diagonalmatrix:
$Qmn =_ <m |Q |n > = qn<m |n> = qndmn$
Wir haben einen Operator mit [,] = und führen nun damit block-diagonale Matrizen ein. Dadurch, daß Q eine Observable ist, gilt:
$0 = <m|[X, Q]| n> = (qn - qm)<m|X|n>$
Damit folgt dann:
$<m |X |n > = 0 fur alle (m,n) mit q /= q ¨ m n$
Darstellungswechsel (beispielsweise für zwei Basissysteme)
|n> mit n = 1, 2, 3, ... sei Eigenvektor der Observable (siehe oben) und |> mit (-,+) Eigenvektor der Observable .
$<q| q'> = d(q- q')$

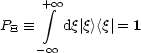
$+ integral o o PE =_ dq|q><q|= 1 - oo$

$integral integral |n> = |q>dq<q|n> =_ |q>dqS(q,n)$

$sum sum |q> = |n ><n|q> =_ |n >T (n,q) n n$
Die Koeffizienten S(,n) bilden eine „Matrix“ mit „Zeilenindex“ und „Spaltenindex“ n. Das Fazit ist nun:
$|---------------------| |T = S†, SS † = S†S = 1 ----------------------$
Daraus folgt, daß die Matrix unitär ist. Erinnern wir uns an folgende Eigenschaft des Skalarprodukts:
$* <q|n> = <n| q>$
Daraus ergibt sich T = S^†.
$sum <q|n><n|q'> = d(q -q') n$
Hieraus folgt SS^† = 1. Analog folgt:
$integral <n| q>dq<q| n'> = dnn'$
Daraus ergibt sich TT^† = 1. Vorsicht ist hier geboten, denn S(,n) ist keine Matrixdarstellung eines Operators, da S(,n) nicht quadratisch ist.

[next] [prev] [prev-tail] [front] [up]