4.3 Hermitesche Operatoren und Observablen

Sei A ein linearer Operator |v> = A|u>. Man nutzt die Relation:

Man kann nun auch einen linearen Operator A definieren, welcher auf Bras wirkt:

Der zu A adjungierte Operator B wird definiert durch die Relation <u|B|w><w|A|u>^* und wird bezeichnet als B = A^†. Es gilt hier auch A^†† = A.

• Konjugationsoperator:

  Man ersetze überall:

  • Zahlen durch konjugiert komplexe Zahlen.
  • Bras durch die dazu konjugierten Kets und umgekehrt
  • Die Operatoren A durch A^†
  • Kehre die Reihenfolge der verschiedenen Symbole um
  • Beispiel 1:

  • Beispiel 2:

  • Beispiel 3:

• Ein linearer Operator H heißt hermitesch, wenn H^† = H ist. H heißt positiv definit, wenn für alle |u>E gilt |<u|H|u>> 0.
• Ein Operator U heißt unitär, wenn UU^† = 1 = U^†U.
• Eigenwertproblem

  Es liege folgende Gleichung vor:

  

  a heißt Eigenwert und |u> Eigenket. Für ein Bra gilt dann analog:

  

  Theorem:

  Ist A hermitesch, so hat man:
  • Beide Eigenwertspektren {a} und {a'} sind identisch: {a} = {a'}.
  • Alle Eigenwerte sind reell, das heißt a .
  • Die Orthogonalität der Eigenvektoren zu verschiedenen Eigenwerten.

    Wir wollen diese Aussage beweisen. Dazu bilden wir das Skalarprodukt mit <v|:

    

    Anschließend führen wir das gleiche Skalarprodukt mit |u> durch:

    

    Durch Subtraktion der beiden Gleichungen ergibt sich dann, da die linke Seite gleich ist:

    

    Für ab gilt dann <v|u> = 0.

• Sei A der hermitesche Operator der Eigenwertgleichung A(x) = a(x) mit diskreten Spektren a_n mit n = 0, 1, 2, ... (möglich mehrfach entartet) und mit kontinuierlichem Anteil a(). Die Eigenfunktionen _n^(r) (r ist Entartungsindex) stellen orthonormierte Kets |n₂> und die Eigenfunktionen ^(r)(,) die Kets |_r>. Die Orthonormierungsrelationen sind:
  
  

  Spannen diese Vektoren den gesamten Raum auf, so sagt man, daß sie ein vollständiges System bilden und daß der hermitesche Operator A eine Observable ist. Wenn dies so ist, dann hat man die Vollständigkeitsrelation.

  

  Man bezeichnet dies als „Zerlegung der Einheit“.

• Projektionsoperatoren

  Gegeben sei der Vektor |v> mit <v|v> = 1. Für jedes |u> haben wir den projektierten Vektor |u_v> = |v><v|u>.

  

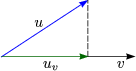
  Wir nennen _v |v><v| den Projektor mit |u_v> = _v|u>. Der Projektor besitzt die Eigenwerte 1 und 0. Für einen linearen Operator  mit normierten Eigenvektoren |a_n> definiert man:

  

  Ein Vektor |u> wird somit auf den durch |a_n> aufgespannten Untervektorraum projiziert. Ist A eine Observable, findet man P_A = 1 (Zerlegung der Einheit).