4.2 Vektoren und Operatoren

• E sei ein linearer Vektorraum mit den Ket-Vektoren |...>, das heißt:

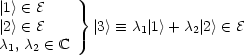
  Oder mit einem kontinuierlichem Index :

  

• Jedem Vektorraum E kann ein dualer Vektorraum E' mit sogenannten Bra-Vektoren <...| zugeordnet werden. Zwischen diesen beiden Vektorräumen E und E' gibt es eine eineindeutige Zuordnung:
  

• Skalarprodukt des Kets |u> mit dem Ket |v> ergibt die Zahl <v|u> . Das Skalarprodukt kann nur definiert sein in einem bestimmten Vektorraum, nämlich dem des Kets oder des Bras. Folgende Eigenschaften sind dabei zu notieren:
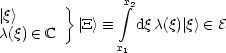
  • <u|v> = <v|u>^*
  • Das Skalarprodukt ist linear.

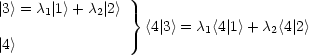
  • Normquadrat: N(u) <u|u>> 0

    Wir wollen an dieser Stelle die Cauchy-Schwarzsche-Ungleichung abführen:

    

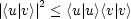
    Das Gleichheitszeichen gilt genau dann, wenn |u> und |v> linear abhängig sind.

• Vollständigkeit und Separabilität

  Liegen diese Eigenschaften vor, handelt es sich um einen Hilbertraum.

• Linearer Operator A

  Ist die Zuordnung eineindeutig, so haben wir zwei Operatoren A und B, so gilt:

  

  A und B heißen invers, wenn AB = 1 und BA = 1. Üblicherweise schreiben wir dann B = A^-1.

• Definition des Tensorprodukts

  Angenommen, wir haben zwei Vektoren |u>¹ E₁ und |v>² E₂. Das Produkt |u¹,v²>|u>¹|v>² E₁ E₂ nennt man Tensorprodukt. Wir haben einen linearen Operator A' im Raum E₁, dann gilt im Produktraum A⁽¹⁾ = A¹ 1².

  

  Ist A⁽²⁾ 1¹ A², so folgt daraus, daß die Operatoren kommutieren: