6.1 Das Problem

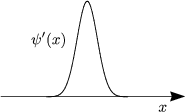
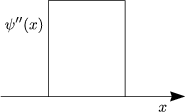
Wir betrachten den Stoß zweier identischer Teilchen. Vor dem Stoß befindet sich ein Teilchen im Zustand ₀'(x) und das andere im Zustand ₀''(x). Diese Wellenfunktionen sollen sich vor dem Stoß nicht überlappen.

|----(1)--(2)----'--1--''--2-| -y0(x--,x--) =_ -y0(x-)y0(x-)

|-----------------------| |y (x1,x2) =_ y''(x1)y'(x2)| --0----------0-----0----

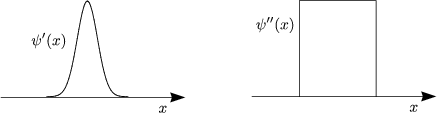
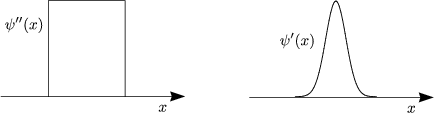
Andererseits definieren wir („S“ bedeutet symmetrisch und „A“ antisymmetrisch):

( ) ( ) y(0S) =_ V~ 1 y0 + y0 , y(0A) =_ V~ 1 y0- y0 2 2

Die allgemeinste Beschreibung des Systems am Anfang ist:

(A) (S) 2 2 Y0 =_ ay 0 + by0 mit |a| = |b| = 1

Man bezeichnet dies als Austauschentartung. Zur Zeit t schreiben wir die Wellenfunktion als:

Y(x1,x2,t) = ay(A) + by(S)

Was ist die Wahrscheinlichkeitsdichte, eines der Teilchen in ' zu finden und das andere in '', lautet:

|-------------------------------------| ' '' ' '' 2 '' ' 2 | 2 || (A) ' '' ||2 2 || (S) ' ''||2| P (x ,x ) = |Y(x ,x )| +|Y(x ,x)| =-2| a|-.|y----(x-,x-)|-+2|b|-.|y---(x,x-)|--

Damit dieser Ausdruck unabhängig von und ist, muß |^(A)(x',x'')| = |^(S)(x',x'')| gelten. Im allgemeinen ist dies jedoch nicht gegeben. Betrachten wir beispielsweise Wellenpakete , welche überlappen: