Betrachten wir N Teilchen {![]() (i),
(i), ![]() (i),
(i), ![]() (i)--i = 1, ..., N}. Diese Teilchen sollen
gleichartig sein (aber nicht identisch). Teilchen bezeichnet man als gleichartig, wenn
für alle i, j gilt, daß die Spins gleich sind:
(i)--i = 1, ..., N}. Diese Teilchen sollen
gleichartig sein (aber nicht identisch). Teilchen bezeichnet man als gleichartig, wenn
für alle i, j gilt, daß die Spins gleich sind: ![]() 2(i) =
2(i) = ![]() 2(j). Dann führen wir folgendes
Tensorprodukt ein. Der Zustandsraum besitze folgende Struktur (Spindimension:
2s + 1).
2(j). Dann führen wir folgendes
Tensorprodukt ein. Der Zustandsraum besitze folgende Struktur (Spindimension:
2s + 1).
Nehmen wir an, wir haben einen vollständigen Satz von kommutierenden
Observablen {q} mit Basisvektoren |q![]() > und den Eigenwerte q (beispielsweise
> und den Eigenwerte q (beispielsweise ![]() ,
sz).
,
sz).
Die Basisvektoren ergeben sich als Tensorprodukt der Einteilchenvektoren. Beschäftigen wir uns nun mit Permutationen. Die einfachste Permutation ist die Transposition, also die Vertauschung zweier benachbarter Elemente:
Der unitäre Permutationsoperator ist nun definiert als:
Das ist eine Art von Quasi-Rotation. Im allgemeinen gilt:
Betrachten wir eine Observable O(![]() (1), ...,
(1), ..., ![]() (N)). Speziell für diese Observable gilt
dann:
(N)). Speziell für diese Observable gilt
dann:
Eine beliebige Permutation P ist zusammengesetzt aus MP Transpositionen P = ()()...()() (MP-fach). Wir wollen außerdem den Begriff der Parität einführen. Die Parität ist folgendermaßen definiert:
Für einen symmetrischen Vektor |u> gilt für beliebiges P, daß P|u> = |u> ist, und für einen antisymmetrischen Vektor |v> gilt P|v> = (-)P|v>. Symmetrische Vektoren ändern sich somit unter Permutationen gar nicht und bei antisymmetrischen nur die Phase.
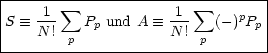
| Sei P1 ein spezieller Projektionsoperator. Dann gilt P1S = SP1 = S und P1A = AP1 = (-)p1A. |